Question

What is the sum of the measures, in degrees, of the interior angles of a 20 – sided polygon?

Answer 1

Hint:Try to form a general expression for calculating the sum of interior angles of a n – sided polygon. Consider the examples of a quadrilateral and a 5 – sided polygon to form the general formula. Consider these shapes one by one and fix a point and see how many triangles can be formed. Use the fact that the sum of interior angles of a triangle is 180 degrees and calculate the sum of interior angles of these shapes. Use the generalized pattern to get the answer for 20 – sided polygons.

Complete step by step solution:
Here we have been asked to find the sum of all the interior angles of a 20 – sided polygon. Let us form a general formula to find the sum of all the interior angles of a n – sided polygon and then there we will substitute n = 20 to get the answer.
Now, let us consider the examples of a quadrilateral and a 5 – sided polygon to form a pattern.
(1) Quadrilateral: We know that a quadrilateral is a 4 – sided polygon. Let us draw its figure.

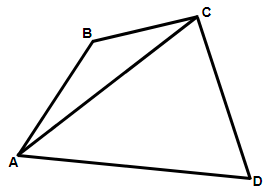
From the above figure we can clearly see that we can form two triangles by fixing a point and considering two points while moving ahead. Now, we know that the sum of the interior angles of a triangle is 180 degrees. Here we have 2 triangles so the sum will be $2\times {{180}^{\circ }}={{360}^{\circ }}$.
(2) 5 – sided polygon: An example of a 5 – sided polygon can be a pentagon. Let us draw its figure.

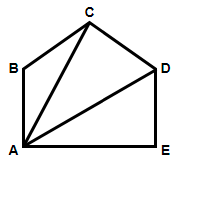
From the above figure we can clearly see that we can form three triangles by fixing a point and considering two points while moving ahead. Using the angle sum property of the triangle we can say that the sum of interior angles of these three triangles will be $3\times {{180}^{\circ }}={{540}^{\circ }}$.
Considering the above two examples we see that when we have 3 sides in a triangle we have the sum of angles equal to $1\times {{180}^{\circ }}$, when there are 4 sides then the sum is $2\times {{180}^{\circ }}$ and when the number of sides is 5 we have the sum $3\times {{180}^{\circ }}$. So according to this pattern if we will have n sides then the sum will be $\left( n-2 \right)\times {{180}^{\circ }}$ which is the general formula for the sum of interior angles of a n – sided polygon.
Now let us come to the question. We have the number of sides equal to 20, so substituting n = 20 in the above formula we get,
\[\begin{align}
 & \Rightarrow \text{Sum}=\left( 20-2 \right)\times {{180}^{\circ }} \\
 & \Rightarrow \text{Sum}=18\times {{180}^{\circ }} \\
 & \therefore \text{Sum}={{3260}^{\circ }} \\
\end{align}\]
Hence the required sum is 3260 degrees.

Note: Always remember the formula $\left( n-2 \right)\times {{180}^{\circ }}$ for the sum of interior angles of n – sided polygon because it will not be proved everywhere but it will be used directly. Also, note that if the polygon is regular that means all the sides are equal then each angle will be equal. Sometimes you may be asked to find each angle. In that case just divide the sum with the number of sides of the polygon.