Question

What is the sum of the exterior angle measures for a regular hexagon?

Answer 1

Hint: Here in this question, we have to find the sum of exterior angle of a regular hexagon. On many occasions a knowledge of exterior angles may throw light on the nature of interior angles and sides. This can be solved by, generalized method and finally we show the sum of the measures of the external angles of the regular hexagon is \[{360^ \circ }\].

Complete step-by-step solution:
Regular polygon is a polygon in which all angles are equal in measure (equiangular) and all sides have the same length (equilateral). Regular polygon either be convex or Star. The Exterior Angle is the angle between any side of a geometrical shape, and a line extended from the next side.
(In other words, when we add interior angle and exterior angle we get a straight line that is \[{180^0}\] then exterior angle = \[{180^0}\]- interior angle).

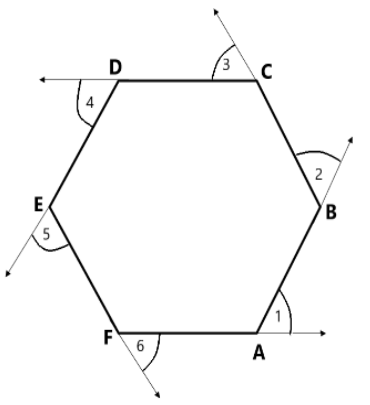
If a hexagon is regular, then all the sides are equal in length, and six angles are of equal measures.
Now, we want to know the total measure of exterior angles of regular hexagon \[ABCDEF\] , i.e., \[m\,\left| \!{\underline {\,
  1 \,}} \right. + m\,\left| \!{\underline {\,
  2 \,}} \right. + m\,\left| \!{\underline {\,
  3 \,}} \right. + m\,\left| \!{\underline {\,
  4 \,}} \right. + m\,\left| \!{\underline {\,
  5 \,}} \right. + m\,\left| \!{\underline {\,
  6 \,}} \right. \]. Start at A. Walk along \[\overline {AB} \]. On reaching B, we need to turn through an angle of \[m\,\left| \!{\underline {\,
  2 \,}} \right. \], to walk along \[\overline {BC} \]. When we reach at C, we need to turn through an angle of \[m\,\left| \!{\underline {\,
  3 \,}} \right. \] to walk along \[\overline {CD} \]. We continue to move in this manner, until we return to side AB. We would have in fact made one complete turn.
Therefore, \[m\,\left| \!{\underline {\,
  1 \,}} \right. + m\,\left| \!{\underline {\,
  2 \,}} \right. + m\,\left| \!{\underline {\,
  3 \,}} \right. + m\,\left| \!{\underline {\,
  4 \,}} \right. + m\,\left| \!{\underline {\,
  5 \,}} \right. + m\,\left| \!{\underline {\,
  6 \,}} \right. = {360^ \circ }\].
Hence, the sum of the measures of the external angles of regular hexagon is \[{360^ \circ }\].

Note: To solve these types of question figures is mandatory and the above solution is true whatever be the number of sides of the polygon either is regular or irregular. Therefore, the sum of the measures of the external angles of any polygon is \[{360^ \circ }\].