Question

Sum of any two sides of a triangle is …………………….. than the third side.
A) Greater
B) Lesser
C) Equal
D) May be greater or lesser

Answer 1

Hint:
The sum of two sides of the triangle is always greater than the other side. In the solution we have to prove this for this firstly we have to consider \[\vartriangle ABC\]. We have to do some construction over it. This construction helps us to prove the solution.

Complete step by step solution:
Consider a \[\vartriangle ABC\]. We have to prove that the sum of two sides of a triangle is always greater than the third side.

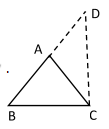
Construction:
Extend AB from point \[A\]up to\[D\]. Then joint\[DC\]. The construction is done such that
\[AD\]= \[AC\]
Prof: In the \[\vartriangle ACD\] Now
In a triangle, angles opposite to the side of the triangle are equal.
Now AC and AD are equal angle opposite to \[AC\] is \[\angle BDC\] and angle opposite to \[AD\] is \[\angle ACD\]
So \[\angle BDC\] = \[\angle ACD\] ……………..(i)
Now \[\angle BCD = \angle BCA + \angle ACD\]
\[\angle BCD = \angle BCA + \angle BDC\] [From (i)]
Now from above we see that \[\angle BCD\] is the sum of \[\angle BCA\] and \[\angle BDC\]. Therefore \[\angle BCD\] is greater than the angle \[\angle BDC\].
Now, in triangle \[BCD\]
\[\angle BCD\] is greater than \[\angle BDC\].
In a triangle side opposite to greater is longer.
So the side opposite to \[\angle BCD\] is \[BD\] and the side opposite to \[\angle BCD\]is \[BD\] and the side opposite to \[\angle BDC\].
So \[BD\] is greater than\[BC\].
Now \[BD = BA + AD\]
Therefore \[AB = AD > BC\]
Since \[AD = AC\]
Therefore \[AD + AC > BC\](By construction).
So the sum of two sides of a triangle is always greater than the third side.
So option \[\left( A \right)\]is correct

Note:
A triangle is a polygon with three edges and three vertices. One of the basic shapes is geometry. The area of triangle is given as
\[Area = \dfrac{1}{2} \times Base \times height\]
Perimeter of triangle = sum of all sides of triangle.
There are different types of triangles like equilateral triangle, right angle triangle isosceles triangle etc.