
Subtract the following on the number line:
A). 9 from 4
B). 9 from -4
C). -8 from3
Answer
543.6k+ views
Hint: In this question, we have to find the values of the given question by solving them on a number line. So, we will use the number line method to get the solution. As we know, if we have to subtract a from b, the mathematical meaning is $b-a$ . Thus, in this problem, we will first draw the number line with 1 unit each. After that, we will mark ‘b’ on the number line and then move a to the left of the b, to get the required solution for the problem.
Complete step-by-step solution:
According to the problem, we have to find the value of each option.
Thus, we will use the number line and the basic mathematical rules.
A). 9 from 4
So, we know that if the statement is in the form $a\text{ from }b$ , then its mathematical term is $b-a$ . thus, here $b=4$ and $a=9$ , which implies we have to find $4-9$ .
Now, we will first draw the number line of each unit, that is

Now, we will go $a$ units left from $b$ , which is 9 units left from the number 4, we get

As we move towards the left, that is we cross number 3, 2, 1, 0, … -4, thus the required answer for the given statement is -5.
B). 9 from -4
So, we know that if the statement is in the form $a\text{ from }b$ , then its mathematical term is $b-a$ . thus, here $b=-4$ and $a=9$ , which implies we have to find $-4-9$ .
Now, we will first draw the number line of each unit, that is
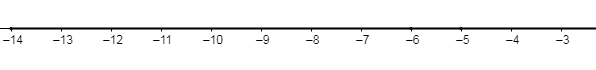
Now, we will go $a$ units left from $b$ , which is 9 units left from the number -4, we get

As we move towards the left, that is we cross number -12,…, -6,-5 , thus the required answer for the given statement is -13.
C). -8 from 3
So, we know that if the statement is in the form $a\text{ from }b$ , then its mathematical term is $b-a$ . thus, here $b=3$ and $a=-8$ , which implies we have to find $3-\left( -8 \right)=3+8$
Now, we will first draw the number line of each unit, that is

Now, we will go $a$ units right from $b$ , which is 8 units right from the number 3, we get

As we move towards right, that is we cross number 4, 5, 6, …, 10 thus the required answer for the given statement is 11.
Therefore, we get the required solution for all the three parts.
Note: While solving this problem, do not forget to draw the number line with 1 unit each. Also, do not confuse writing the statement $a\text{ from }b$, it is equal to $b-a$ and not $a-b$ . Always remember that when we subtract, we will go to the left of the number and when we add, we will go right of the number.
Complete step-by-step solution:
According to the problem, we have to find the value of each option.
Thus, we will use the number line and the basic mathematical rules.
A). 9 from 4
So, we know that if the statement is in the form $a\text{ from }b$ , then its mathematical term is $b-a$ . thus, here $b=4$ and $a=9$ , which implies we have to find $4-9$ .
Now, we will first draw the number line of each unit, that is

Now, we will go $a$ units left from $b$ , which is 9 units left from the number 4, we get

As we move towards the left, that is we cross number 3, 2, 1, 0, … -4, thus the required answer for the given statement is -5.
B). 9 from -4
So, we know that if the statement is in the form $a\text{ from }b$ , then its mathematical term is $b-a$ . thus, here $b=-4$ and $a=9$ , which implies we have to find $-4-9$ .
Now, we will first draw the number line of each unit, that is
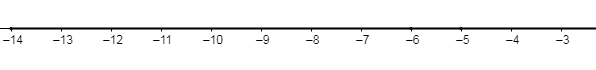
Now, we will go $a$ units left from $b$ , which is 9 units left from the number -4, we get

As we move towards the left, that is we cross number -12,…, -6,-5 , thus the required answer for the given statement is -13.
C). -8 from 3
So, we know that if the statement is in the form $a\text{ from }b$ , then its mathematical term is $b-a$ . thus, here $b=3$ and $a=-8$ , which implies we have to find $3-\left( -8 \right)=3+8$
Now, we will first draw the number line of each unit, that is

Now, we will go $a$ units right from $b$ , which is 8 units right from the number 3, we get

As we move towards right, that is we cross number 4, 5, 6, …, 10 thus the required answer for the given statement is 11.
Therefore, we get the required solution for all the three parts.
Note: While solving this problem, do not forget to draw the number line with 1 unit each. Also, do not confuse writing the statement $a\text{ from }b$, it is equal to $b-a$ and not $a-b$ . Always remember that when we subtract, we will go to the left of the number and when we add, we will go right of the number.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Difference Between Plant Cell and Animal Cell

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Who is eligible for RTE class 9 social science CBSE

Which places in India experience sunrise first and class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Name 10 Living and Non living things class 9 biology CBSE




