Question

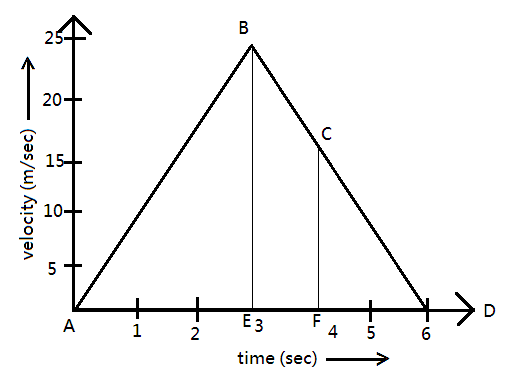
Study the velocity-time graph and calculate.
A. The acceleration from A to B
B. The acceleration from B to C
C. The distance covered in the region ABE
D. The average velocity from C to D
E. The distance covered in the region BCFE

Answer 1

Hint: There are five sub parts of this question, read each sub-part carefully and then solve the problem. The slope of the velocity time graph is acceleration. To find the distance covered using a kinematical equation, we have velocity, time and acceleration to distance travelled can be easily calculated.

Complete step by step answer:
The given diagram depicts a motion in which a particle starts from point A at time $t = 0$ and then it accelerates till it reaches point B. From point B the particle decelerates till $t = 6s$ . On the X-axis we have time and, on the Y-axis, we have velocity.
As we have discussed in the hint section, acceleration is the slope of the velocity time graph.
Also, we have the kinematical equation, $v - u = at$
Here $v$ is the final velocity, $u$ is the initial velocity, $t$ is the time taken and $a$ is the acceleration.
From this equation, we can have
$a = \dfrac{{v - u}}{t}$
From the graph we have the following values when the particle travels from A to B.
$v = 25\,m{s^{ - 1}}$ , $u = 0m{s^{ - 1}}$ and $t = 3s$ , substituting these values in the above equation, we have
$a = \dfrac{{25 - 0}}{3}$
$ \Rightarrow a = \dfrac{{25}}{3} = 8.33m{s^{ - 2}}$
Therefore, the acceleration from A to B is $8.33m{s^{ - 2}}$ .
The acceleration from B to C.
From the graph we have the following values when the particle travels from B to C.
$v = 20m{s^{ - 1}}$ , $u = 25m{s^{ - 1}}$ and $t = 1s$ , substituting these values in the above equation, we have
$a = \dfrac{{20 - 25}}{1}$
$ \Rightarrow a = - 5m{s^{ - 2}}$
The acceleration from B to C is $ - 5m{s^{ - 2}}$ .
The negative sign implies that the body is decelerating.
Distance covered in region ABE.
Distance covered is given as the area under the velocity time graph.
Distance covered $s$ will be given as
$s = Area\left( {\vartriangle ABE} \right)$
$ \Rightarrow s = \dfrac{1}{2} \times 3 \times 25$
$ \Rightarrow s = 37.5m$
The distance travelled in the region ABE is $37.5m$ .
The average velocity from C to D.
The average velocity will be
${v_{avg}} = \dfrac{{20}}{2}$
${v_{avg}} = 10m{s^{ - 1}}$
The average velocity from C to D is $10m{s^{ - 1}}$ .
Distance covered in the region BCFE
Distance will be given as the area under BCFE region, the BCFE region comprises of triangle with height $5m$ , base $EF = 1m$ and a rectangle have having length $CF = 20m$ and breadth $EF = 1m$
The distance covered $s$ will be equal to the total area, it will be given as
$s = \dfrac{1}{2} \times 1 \times 5 + 20 \times 1$
$ \Rightarrow s = 22.5m$
The distance covered in the region BCFE is $22.5m$ .
Thus, a) the acceleration from A to B is $8.33m{s^{ - 2}}$
b) acceleration from B to C is $ - 5m{s^{ - 2}}$ .
c) The distance travelled in the region ABE is $37.5m$ .
d) The average velocity from C to D is $10m{s^{ - 1}}$ .
e) The distance covered in the region BCFE is $22.5m$.

Note:
The area under the velocity-time graph gives the distance travelled.
The slope of the velocity-time graph gives the magnitude as well as the direction of the acceleration.
If the slope of the velocity-time graph is positive, the body is accelerating else the body is not accelerating.