Question

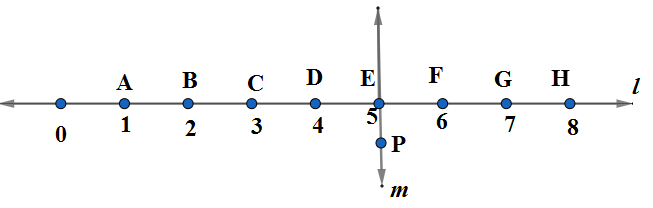
Study the diagram. The line $l$ is perpendicular to line $m$. Are these true?
(a) $CD=GH$(b) Does $PE$ bisect $CG$ ? \[\]

Answer 1

Hint: We recall the point and line segment of geometry. We see in the figure that each point is named by a letter and a designated number. We find the distance between two points as the number of points we cross when we move from the initial point to the final point. We recall the definition of bisection which means dividing a line segment into two line segments of equal length. \[\]

Complete step by step answer:
We know that a point is a basic geometrical shape that is always named by a letter from the English alphabet. We also know that a line segment is a part of the line which is bounded by two endpoints. The length of a line segment is the distance between two endpoints. \[\]

We see in the given figure that we are given 8 points A, B, C, D, E, F, G, and H which have numerical values right below them as 1,2,3,4,5,6,7,8 respectively\[\]
(a) We are asked if $CD=GH$ is true. We see in the figure that when we from C to D we only move by 1 point. So the length of the line segment is $CD=1$. Similarly, if we move from G to H we move by 1 point, so the length is $GH=1$. SO it is true that $CD=GH$. \[\]
(b) We are asked if PE bisects CG. We know that the bisection of line segment means dividing a line segment into two line segments of equal length. PE which is on the perpendicular line $m$divides CG into two line segments CE and GE. We move for C to E and find the distance of $CE=2$. Similarly, we move from E to G and find a distance of $GE=2.$Since $CE=GE$ it is true PE bisects CG.\[\]

Note:
We can alternatively solve using the concept of absolute value where we first denote the numerical values as $A=1,B=2,C=3,D=4,E=5,F=6,G=7,H=8$. We find the distance between two points as $\left| x-y \right|$ where $x,y$ are the numerical values of those points. We must always exclude the final point when we are finding the distance by counting.