Question

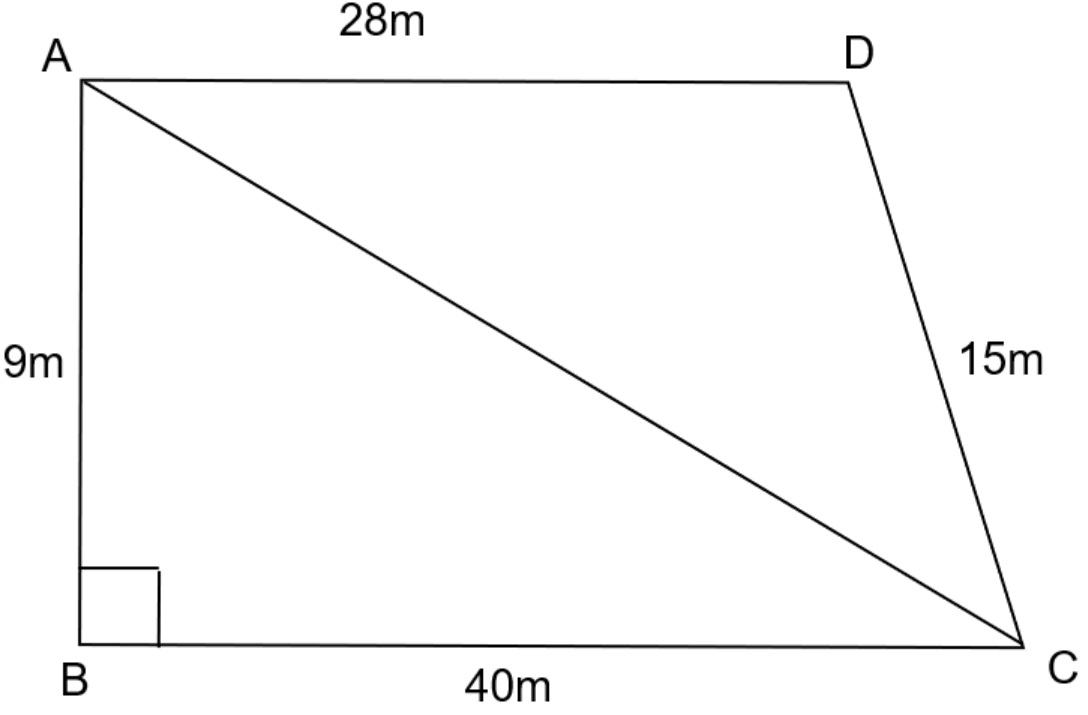
Students of a school staged a rally for a cleanliness campaign. They walked through the lanes in two groups. One group walked through the lanes \[AB\], \[BC\] and \[CA\] where the other went through \[AC\], \[CD\] and \[DA\]. Then they cleaned the area enclosed within their lanes. If \[AB = 9m\], \[BC = 40m\], \[CD = 15m\], \[DA = 28m\] and , which group cleaned more area and by how much ? Find the total area cleaned by the students.

Answer 1

Hint: We have to find which of the two groups cleaned more areas and what is the difference between the two areas. Also we have to find the total area cleaned by both the groups. We solve this question using the concept of area of triangles. We should have the knowledge of the formula of the area of triangles using the sides and the semi - perimeter of the triangle. First, we will find the areas of the two triangles by using different methods of area of triangles. The area of \[\Delta ABC\] by using area of perpendicular triangle and the area of \[\Delta ADC\] by using the formula of area of triangles using semi - perimeter of the triangle. Then we will compare the areas of the two triangles and then we will state which group cleaned more areas and hence find the difference between the two areas. And finally we find the total area cleaned by the two groups by summing the area cleaned by both the groups.

Complete step-by-step solution:
Given :
\[AB = 9m\], \[BC = 40m\], \[CD = 15m\], \[DA = 28m\] and
We know that area of triangle is given as :
\[area = \dfrac{1}{2} \times base \times height\]
Area of \[\Delta ABC\] is given as :
\[are{a_1} = \dfrac{1}{2} \times 9 \times 40\]
On solving, we get
\[are{a_1} = 180{m^2}\]
Now we know that the pythagoras formula is given as :
\[{\left( {base} \right)^2} + {\left( {perpendicular} \right)^2} = {\left( {hypotenuse} \right)^2}\]
Now, using this formula we can find the value of \[AC\] as :
\[{(BC)^2} + {(AB)^2} = {(AC)^2}\]
Putting the values, we get
\[{(40)^2} + {(9)^2} = {(AC)^2}\]
\[{(AC)^2} = 1600 + 81\]
Further, we get
\[{(AC)^2} = 1681\]
\[AC = 41{\text{ }}m\]
We also know that the area of the triangle is given as :
\[area = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} \]
[Where \[s\] is the semi - perimeter of the triangle and \[a\], \[b\] and \[c\] are the sides of the triangles]
Now, using the formula we can calculate the area of the \[\Delta ADC\].
\[Perimeter{\text{ }}of\Delta ADC = AD + DC + AC\]
\[Perimeter{\text{ }}of\Delta ADC = 28 + 15 + 41\]
On solving, we get
\[Perimeter{\text{ }}of\Delta ADC = 84\]
Putting value of perimeter in the formula of semi perimeter, we get
\[s = \dfrac{{84}}{2}\]
\[s = 42m\]
Putting the values in the formula of area, we get
\[are{a_2} = \sqrt {s\left( {s - AD} \right)\left( {s - DC} \right)\left( {s - AC} \right)} \]
\[are{a_2} = \sqrt {42\left( {42 - 28} \right)\left( {42 - 15} \right)\left( {42 - 41} \right)} \]
On solving, we get
\[are{a_2} = \sqrt {42 \times 14 \times 27 \times 1} \]
We can write the value of area as :
\[are{a_2} = \sqrt {15876} \]
\[are{a_2} = 126{m^2}\]
Hence, On comparing the two areas we conclude that students of group \[1\] cleaned more areas than students of group \[2\].
The difference in the area of the two groups is :
\[are{a_1} - are{a_2} = 180 - 126\]
\[are{a_1} - are{a_2} = 54{m^2}\]
The total area cleaned is given as :
\[Total{\text{ }}area = are{a_1} + are{a_2}\]
\[Total{\text{ }}area = 180 + 126\]
On solving, we get
\[Total{\text{ }}area = 306{m^2}\]
Hence, the total area cleaned by the students is \[306{m^2}\].

Note: We used two different formulas of the area of the triangle, as according to the given condition. In the \[\Delta ABC\] it is given that one of the angles is a right angled triangle so we can use the formula used as \[\dfrac{1}{2} \times base \times height\]. We can use the formula of area of triangle using semi - perimeter in any type of triangle where the other triangle is not a right angled triangle. Here we could also used the Determinant for finding the area of a triangle if we would have given the vertices of a triangle.