Question

(Street Plan): A city has two main roads which cross each other at the center of the city. These two roads are along the North-South direction and the East-West direction. All the other streets of the city-run parallel to these roads and are $200m$ apart. There are $5$ streets in each direction. Using $1cm=200m,$ draw a model of the city on your notebook. Represent the roads/streets by single lines. There are many cross-streets in your model. A particular cross-street is made by two streets, one running in the North-South direction and another in the East-West direction. Each cross street is referred to in the following manner: If the ${{2}^{nd}}$ street running in the North-South direction and ${{5}^{th}}$ in the East-West direction meet at some crossing, then we will call this cross-street $\left( 2,5 \right).$ Using this conversion, find:
\[\left( i \right)\] How many cross-streets can be referred to as $\left( 4,3 \right)$
$\left( ii \right)$ How many cross-streets can be referred to as $\left( 3,4 \right).$

Answer 1

Hint: We know that if there are cross-streets referred to as $\left( m,n \right),$ then that means the ${{m}^{th}}$ street running in the North-South direction and the ${{n}^{th}}$ street running in the East-West direction meet at some crossing.

Complete step by step answer:
Let us draw a model of the city as follows,

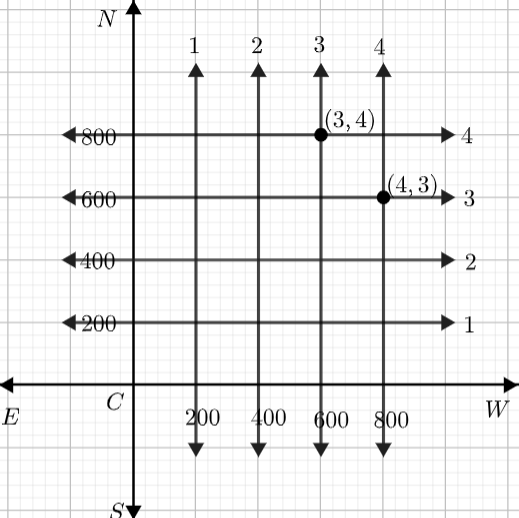
We can see many cross-streets in the model. We are asked to find
\[\left( i \right)\] the number of cross-streets that can be referred to as $\left( 4,3 \right)$
$\left( ii \right)$ the number of cross-streets that can be referred to as $\left( 3,4 \right)$
So, as we can see, the ${{4}^{th}}$ street running in the North-South direction and the ${{3}^{rd}}$ street running in the East-West direction meet at $\left( 4,3 \right).$ So, there is only one cross-street we can refer to as $\left( 4,3 \right).$
Similarly, we can see that the ${{3}^{rd}}$ street running in the North-South direction and the ${{4}^{th}}$ street running in the East-West direction meet at $\left( 3,4 \right).$ So, there is only one cross-street we can refer to as $\left( 3,4 \right).$
Hence the cross-streets that can be referred to as $\left( 4,3 \right)$ and $\left( 3,4 \right)$ are uniquely found.

Note: As we know, the street plan is a map of a town or city, showing the position and names of all the streets. Here, we use a model of the city that contains streets in the North-South direction and East-West direction. The horizontal lines and the vertical lines we draw are the streets and if the lines meet at some points, then the streets are called cross-streets and referred to as the point at which they meet.