Question

What is the steady current in the $ 2\Omega $ resistor shown in the figure? The internal resistance of the battery is negligible and the capacitance $ C = 0.5\mu F $

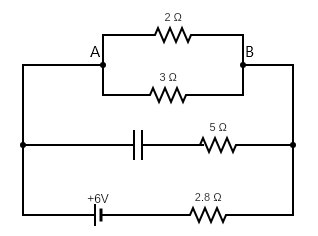
(A) $ 0.3{\text{A}} $
(B) $ 0.6{\text{A}} $
(C) $ 0.9{\text{A}} $
(D) $ 1.2{\text{A}} $

Answer 1

Hint: A capacitor does not allow steady current (direct current) to flow through it and hence acts as an open circuit. The 2 ohms and 3 ohms are resistors connected in parallel. So we need to calculate the equivalent resistance from the rest of the arms and then using Kirchhoff’s law we can calculate the current.

Formula used: In this solution we will be using the following formula;
 $ V = IR $ where $ V $ is the potential difference across a resistor, $ I $ is the current flowing through it and $ R $ is the resistance of the resistor
 $ \dfrac{1}{{{R_p}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} +... + \dfrac{1}{{{R_n}}} $ where $ {R_p} $ is the equivalent resistance of a parallel arrangement of resistors and $ {R_1}...{R_n} $ are the individual resistors in the parallel arrangement.

Complete step by step answer
To calculate the current flowing through the 2 ohms resistor, we have to calculate the potential difference across it. Now, the 2 ohms and 3 ohms resistors are in parallel, hence the same potential is across them. The equivalent resistance can be given as
 $ \dfrac{1}{{{R_{2,3}}}} = \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}} $ where $ {R_{2,3}} $ is the equivalent resistance of the 2 and 3 ohms resistor. $ {R_2} $ and $ {R_3} $ are the 2 ohms and 3 ohms resistance respectively. Hence
 $ \dfrac{1}{{{R_{2,3}}}} = \dfrac{1}{2} + \dfrac{1}{3} = \dfrac{{3 + 2}}{6} = \dfrac{5}{6} $
Hence, by inversion, we get
 $ {R_{2,3}} = \dfrac{6}{5} = 1.2\Omega $
Since there is a capacitor in the middle branch, the middle branch can be eliminated since a capacitor will act as an open circuit. Current will not flow through the branch.
Then, the $ 1.2\Omega $ is in series with the $ 2.8\Omega $
We can apply Kirchhoff’s voltage rule across the loop as in
 $ V - I{R_{2,3}} - I{R_{2.8}} = 0 $ where $ V $ is the voltage of the battery, and $ {R_{2.8}} $ is the resistance of the $ 2.8\Omega $ resistor, and $ I $ is the current flowing through the equivalent circuit.
Hence, by inserting the known values
 $ 6 - I\left( {1.2} \right) - I(2.8) = 0 $
 $ \Rightarrow 6 = I\left( {1.2 + 2.8} \right) = 4.0I $
Then, the current
 $ I = \dfrac{6}{{4.0}} = 1.5A $
Then the voltage across AB is
 $ {V_{AB}} = I{R_{2,3}} = 1.5(1.2) = 1.8{\text{V}} $
Then the current through 2 ohms resistor will be
 $ {I_2} = \dfrac{{{V_{AB}}}}{{{R_2}}} = \dfrac{{1.8}}{2} = 0.9A $
Hence, the correct answer is C.

Note
For clarity, the capacitor does not allow direct current to pass through it because, really, the capacitor is just two conductors placed in proximity to one another, without actually touching. Hence, this causes a break in the circuit.