Question

Statement-1: Perpendicular from point $A\left( 1,1 \right)$ to the line joining he points $B\left( c\cos \alpha ,c\sin \alpha \right)$ and $C\left( c\cos \beta ,c\sin \beta \right)$ bisects BC for all values of $\alpha $and $\beta $.
Statement-2: perpendicular drawn from the vertex to the base of an isosceles triangle bisects the base.
(a). Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1.
(b). Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1.
(c). Statement 1 is true, statement 2 is false.
(d). Statement 1 is false, statement 2 is false.

Answer 1

Hint: We know the perpendicular from vertex to base of an isosceles triangle will bisect the side. By general knowledge of geometry, the two sides are equal in an isosceles triangle, so the corresponding angles will also be equal. So, in the first statement if we prove it is an isosceles triangle then one statement will be completed. For that measure 2 sides of the triangle and prove them equal. Distance formula: By basic knowledge we can say distance (d) between the points $\left( a,b \right)$, $\left( c,d \right)$ is given by
$d\ =\ \sqrt{{{\left( a-c \right)}^{2}}+{{\left( b-d \right)}^{2}}}$.

Complete step-by-step answer:
Proof for condition: -
In an isosceles triangle 2 sides are equal.

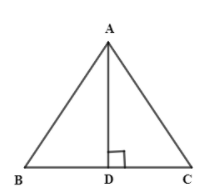
Let the 2 equal sides be AB, AC.
By corresponding angles of equal condition, we get angle B is equal to angle C.
If AD is perpendicular, we have angle \[ADB={{90}^{\circ }}\] and angle \[ADC={{90}^{\circ }}\].
In triangles ADB and ADC, 2 sides, one is AD and other isosceles triangles are equal and also angle 90 is the same.
So, by SAS axiom we can say,
\[\text{BD=DC}\]
So, perpendicular from vertex to base in an isosceles triangle bisects it.
Here point A is given by co-ordinates \[\left( 1,1 \right)\], B is given by co-ordinates $\left( c\cos \alpha ,c\sin \alpha \right)$, C is given by $\left( c\cos \beta ,c\sin \beta \right)$.
Distance (d) between \[\left( a,b \right)\], \[\left( c,d \right)\] is given by formula.
$d\ =\ \sqrt{{{\left( c-a \right)}^{2}}+{{\left( b-d \right)}^{2}}}$
By applying this to AB we have \[\left( 1,1 \right)\], $\left( c\cos \alpha ,c\sin \alpha \right)$, we get:
$=\ \sqrt{{{\left( 1-c\cos \alpha \right)}^{2}}+{{\left( 1-c\sin \alpha \right)}^{2}}}$
By applying this to AC we have \[\left( 1,1 \right)\], $\left( c\cos \beta ,c\sin \beta \right)$ we get:
$=\ \sqrt{{{\left( 1-c\cos \beta \right)}^{2}}+{{\left( 1-c\sin \beta \right)}^{2}}}$
So, the distance depends on \[\alpha ,\beta \] , so it is not bisecting the line for all \[\alpha ,\beta \].
As we failed to ABC is isosceles so we say that perpendicular from A does not bisect the BC for all angles \[\alpha ,\beta \].
So, statement-1 is false statement-2 is true.
Hence, option (d) is correct.

Note: Be careful while calculating the distance. See, whether it depends on angle or not. If it depends on angle then write false. The statement saying it depends on both angles is very important. Because that statement paves the way for proving that statement 1 is false. Apply the distance formula carefully, because students generally confuse and forget to write the square term.