Question

Statement-1: Orthocentre of $\Delta $ where vertices are $\left( 8,2 \right),\left( 2,2 \right)\And \left( 8,6 \right)\text{ is }\left( 2,-2 \right).$
Statement-2: If $\Delta $ is right-angled $\Delta $ , then the orthocentre of $\Delta $ is the vertex having angle $90{}^\circ $.
A) Statement $1$ is true, statement $2$ is true; statement $2$ is the correct explanation for statement $1$.
B) Statement $1$ is true, statement $2$ is true; statement $2$ is not the correct explanation for statement $1$ .
C) Statement $1$ is true, statement $2$ is false.
D) Statement $1$ is false, statement $2$ is true.

Answer 1

Hint: Centroid is the point of intersection of medians of a triangle.
Orthocentre is the point of intersection of altitudes of a triangle.
Circumcentre is the point of intersection of the perpendicular bisectors of the sides of a triangle.

Complete step-by-step answer:
Statement$1$:
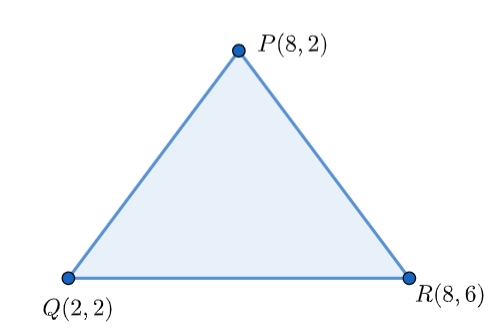
Let the vertices of the triangle be $P\left( 8,2 \right),Q\left( 2,2 \right)$ and $R\left( 8,6 \right)$.

Now, we know the slope of the line joining $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is given as $m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ .
So, the slope of $PQ={{m}_{PQ}}=\dfrac{2-2}{2-8}=0$ .
The slope of $PR={{m}_{PR}}=\dfrac{2-6}{8-8}=\infty $ .
Now, $PQ\And PR$ are perpendicular to each other. Hence, the triangle is right-angled . Now, we know in a right-angled triangle, the circumcentre is the midpoint of the hypotenuse .
Now, we will find the circumcentre, i.e. the midpoint of the hypotenuse.
We know, the midpoint of the line joining two points $\left( {{a}_{1}},{{b}_{1}} \right)$ and $\left( {{a}_{2}}{{b}_{2}} \right)$ is given as
$\left( \dfrac{{{a}_{1}}+{{a}_{2}}}{2},\dfrac{{{b}_{1}}+{{b}_{2}}}{2} \right)$
So, the midpoint of hypotenuse $QR$ is $\left( \dfrac{2+8}{2},\dfrac{2+6}{2} \right)$ .
$=C\left( 5,4 \right)$
Hence, the circumcentre of $\Delta PQR$ is $C\left( 5,4 \right)$ .
Now, we will find the centroid of $\Delta PQR$ .
We know the centroid of $\Delta $ with vertices \[\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}}{{y}_{2}} \right)\] and \[\left( {{x}_{3}}{{y}_{3}} \right)\] is given by:
$G\left( \dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\dfrac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)$.
Hence, the centroid of $\Delta PQR$ is given by:
_{$G\left( \dfrac{8+2+8}{3},\dfrac{2+2+6}{3} \right)$}
$=G\left( 6,\dfrac{10}{3} \right)$
Now, let the orthocentre of the triangle be $O\left( h,k \right)$ . We know, the centroid of a triangle divides the line joining orthocentre and circumcentre is the ratio $2:1$ .
Now, we know, if a point $\left( x,y \right)$ divides the line joining $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ in the ratio $m : n$, then
$\left( x,y \right)=\left( \dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right)$.
So, $\left( 6,\dfrac{10}{3} \right)=\left( \dfrac{\left( 1\times h \right)+\left( 2\times 5 \right)}{3},\dfrac{1\times k+\left( 2\times 4 \right)}{3} \right)$ .
Now, $6=\dfrac{h+10}{3}\Rightarrow h=8$
And $\dfrac{10}{3}=\dfrac{k+8}{3}\Rightarrow k=2$
So, the coordinates of orthocentre are $\left( 8,2 \right)$ .
Statement $2$ :
In a right-angled triangle, two sides are perpendicular to each other. Hence, they will be the altitudes and the meet at the vertex with $90{}^\circ $ angle.
Hence, the vertex with $90{}^\circ $ angle will be the orthocentre.
Hence, the correct option is option (d).

Note: The midpoint of the line joining the points$\left( {{x}_{1}},{{y}_{1}} \right)\text{ and }\left( {{x}_{2}},{{y}_{2}} \right)$ is given as:
$\left( \dfrac{\left( {{x}_{1}}+{{x}_{2}} \right)}{2},\dfrac{\left( {{y}_{1}}+{{y}_{2}} \right)}{2} \right)$ and not $\left( \dfrac{\left( {{x}_{1}}-{{x}_{2}} \right)}{2},\dfrac{\left( {{y}_{1}}-{{y}_{2}} \right)}{2} \right)$ . Students often get confused between the two. Due to this confusion, they generally end up getting a wrong answer. So, such mistakes should be avoided.