Question

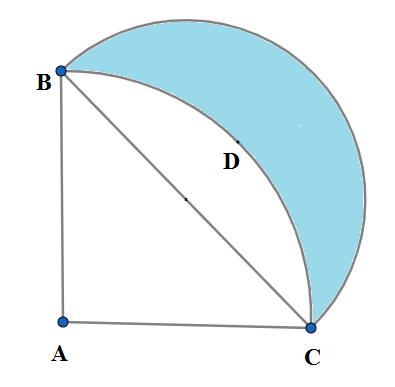
Statement-1: ABDC is a quadrant of circle with centre A and radius 14 cm. A semicircle is drawn with BC as a diameter and then the area of the shaded region is $49\text{ c}{{\text{m}}^{2}}$. \[\]
Statement-2: The required area is $=\dfrac{\pi }{8}{{\left( BC \right)}^{2}}-\left[ \dfrac{\pi }{4}{{\left( AC \right)}^{2}}-\dfrac{1}{2}AC\cdot AB \right]$ \[\]

A. Statement-1 is True, Statement-2 is True and Statement-2 is a correct explanation for Statement-1. \[\]
 B. Statement-1 is True, Statement-2 is True and Statement-2 is not a correct explanation for Statement-1. \[\]
 C. Statement-1 is True, Statement-2 is false. \[\]
 D. Statement-1 is False, Statement-2 is true. \[\]

Answer 1

Hint: We check whether statement-2 is true or false by finding the expression of the area of the shaded region in terms of the sides of triangle ABC. We find the area of the shaded region as the area of the semicircle minus the area of the quadrant ABCD plus the area of the triangle ABC. We put the lengths of the sides AB, AC, BC in the expression to check whether statement-1 is true or not.

Complete step-by-step solution:
We are given in the figure ABDC a quadrant of the circle with center A and radius 14 cm. So we have the equal radii
\[AB=AC=14\text{ cm}\]
So the triangle ABC is an isosceles right-angled triangle with hypotenuse BC. We know that in an isosceles right-angled triangle the circum-center lies on the midpoint of the hypotenuse. Let E be the midpoint of hypotenuse BC. So E is the center of a semicircle drawn taking BC as diameter. Let F be a point on that semi-circle. \[\]
We can find the area of the shaded region BDCF by subtracting the area of the segment BCD from the area of the semicircle BFC. We can find the area of the segment BCD by subtracting the area of the triangle ABC from the area of the quadrant ABDC. So we have;
\[\begin{align}
  & \text{Area of shaded region}=\text{Area of semicircle BFC}-\text{Area of BECD} \\
 & \Rightarrow \text{Area of shaded region}=\text{Area of semicircle BFC}-\left( \text{Area of quadrant ABDC}-\text{Area of }\Delta \text{ABC } \right) \\
\end{align}\]
We know that the area of a semicircle is half the area of a circle that is$\dfrac{1}{2}\pi {{r}^{2}}$. The diameter of the semi-circle BFC is BC so the radius is $\dfrac{BC}{2}$. So the area of the semicircle BFC is;
\[\begin{align}
  & \text{Area of semicircle BFC}=\dfrac{1}{2}\times \pi \times {{r}^{2}} \\
 & \Rightarrow \text{Area of semicircle BFC}=\dfrac{\pi }{2}\times {{\left( \dfrac{BC}{2} \right)}^{2}} \\
 & \Rightarrow \text{Area of semicircle BFC}=\dfrac{\pi }{2}\times \dfrac{{{\left( BC \right)}^{2}}}{4} \\
 & \Rightarrow \text{Area of semicircle BFC}=\dfrac{\pi }{8}{{\left( BC \right)}^{2}} \\
\end{align}\]

The area of the quadrant is one-fourth of the area of the circle that is $\dfrac{1}{4}\pi {{r}^{2}}$. The radius of the quadrant ABDC is AC. So we have
\[\begin{align}
  & \text{Area of quadrant ABDC}=\dfrac{1}{4}\pi {{r}^{2}} \\
 & \Rightarrow \text{Area of quadrant ABDC}=\dfrac{\pi }{4}{{\left( AC \right)}^{2}} \\
\end{align}\]
The area of a right angled triangle is half of the product of sides making the right angle. We see in triangle ABC, the sides AB and AC make the right triangle. So we have;
\[\text{Area of }\Delta \text{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\]
Then we have;
\[\begin{align}
  & \text{Area of shaded region}=\text{Area of semicircle BFC}-\left( \text{Area of quadrant ABDC}-\text{Area of }\Delta \text{ABC } \right) \\
 & \Rightarrow \text{Area of shaded region}=\dfrac{\pi }{8}{{\left( BC \right)}^{2}}-\left( \dfrac{\pi }{4}{{\left( AC \right)}^{2}}-\dfrac{1}{2}\cdot \text{AC}\cdot \text{AB } \right) \\
\end{align}\]So statement-II is correct . Since we are given the radius $AB=AC=14$ cm and we use Pythagoras theorem in triangle ABC to find hypotenuse
\[\begin{align}
  & BC=\sqrt{A{{C}^{2}}+A{{B}^{2}}} \\
 & \Rightarrow BC=\sqrt{{{14}^{2}}+{{14}^{2}}} \\
 & \Rightarrow BC=14\sqrt{2}\text{ cm} \\
\end{align}\]
We put $AB=AC=14\text{ cm},BC=14\sqrt{2}\text{ cm}$ in expression for area and have ;
\[\begin{align}
  & \text{Area of shaded region}=\dfrac{\pi }{8}{{\left( 14\sqrt{2} \right)}^{2}}-\left( \dfrac{\pi }{4}{{\left( 14 \right)}^{2}}-\dfrac{1}{2}\times 14\times 14 \right) \\
 & \Rightarrow \text{Area of shaded region}=\dfrac{22}{8\times 7}\times 14\times 14\times 2-\left( \dfrac{22}{4\times 7}14\times 14-\dfrac{1}{2}\times 14\times 14 \right) \\
 & \Rightarrow \text{Area of shaded region}=154-\left( 154-98 \right)=98\text{ c}{{\text{m}}^{2}} \\
\end{align}\]
So statement-1 is false. Hence the correct option is D.

Note: We should always find the true value of the second statement in assertion reason type questions. We must properly use units of area and lengths. The Pythagoras theorem states that in a right-angled triangle the square of the hypotenuse is the sum of squares of the other two sides. We can find the area of any sector that has central angle $\theta $ as $A=\dfrac{\theta }{2}{{r}^{2}}$ and we can find the area of circular segment whose arc makes an central angle $\theta $as $A=\dfrac{\theta -\sin \theta }{2}{{r}^{2}}$.