Question

Statement I: The equation ${\left( {{{\sin }^{ - 1}}x} \right)^3} + {\left( {{{\cos }^{ - 1}}x} \right)^3} - a{\pi ^3} = 0$ has a solution for all $a \geqslant \dfrac{1}{{32}}$.
Statement II: For any $x \in \mathbb{R},{\text{ }}{\sin ^{ - 1}}x + {\cos ^{ - 1}}x = \dfrac{\pi }{2}$ and $0 \leqslant {\left( {{{\sin }^{ - 1}}x - \dfrac{\pi }{2}} \right)^2} \leqslant \dfrac{{9{\pi ^2}}}{{16}}.$
A) Both statements I and II are true.
B) Both statements I and II are true but I is not a correct explanation of II
C) Statement I is true and statement II is false
D) Statement I is false and statement II is true

Answer 1

Hint: Reduce the given equation using the inverse trigonometric identity.
Roots (or solution) of an equation of variable $x$, is the value of $x$ which satisfies the equation.
The nature of the roots of a quadratic equation is determined by the value of the discriminant, denoted by D.
The discriminant of the quadratic equation $a{x^2} + bx + c$ would be ${b^2} - 4ac$ here, a,b and c are coefficients of the equation.
$D = {b^2} - 4ac$ (a, b and c are coefficients of the quadratic equation)
If $D < 0$, Equation would have complex roots (real part+ imaginary part)
If $D > 0$, Equation would have two distinct real roots
If $D = 0$, Equation would have two real and equal roots.
We consider the existence of a solution when the solution is real.
The domain of the function $f\left( x \right)$ , is a set of all values of x for which the function is valid. The range is the set of all output values of the function.

Complete step-by-step answer:
Step 1: Analysing statement I
Given equation: ${\left( {{{\sin }^{ - 1}}x} \right)^3} + {\left( {{{\cos }^{ - 1}}x} \right)^3} - a{\pi ^3} = 0$
Take ${\sin ^{ - 1}}x = t$
Using inverse trigonometric identity:
${\sin ^{ - 1}}x + {\cos ^{ - 1}}x = \dfrac{\pi }{2}$
$\because {\cos ^{ - 1}}x = \dfrac{\pi }{2} - {\sin ^{ - 1}}x$
Therefore, in terms of ‘t’, ${\cos ^{ - 1}}x = \dfrac{\pi }{2} - t$
Substituting in the given equation.
\[{\left( t \right)^3} + {\left( {\dfrac{\pi }{2} - t} \right)^3} - a{\pi ^3} = 0\] …… (1)
Expand \[{\left( {\dfrac{\pi }{2} - t} \right)^3}\] using identity ${\left( {a - b} \right)^3}$
i.e. ${\left( {a - b} \right)^3} = {a^3} - {b^3} - 3{a^2}b + 3a{b^2}$
on comparing, $a = \dfrac{\pi }{2},b = t$
$
  {\left( {\dfrac{\pi }{2} - t} \right)^3} = {\left( {\dfrac{\pi }{2}} \right)^3} - {t^3} - 3{\left( {\dfrac{\pi }{2}} \right)^2}t + 3 \times \dfrac{\pi }{2}{t^2} \\
   \Rightarrow {\dfrac{\pi }{8}^3} - {t^3} - {\dfrac{{3\pi }}{4}^2}t + \dfrac{{3\pi }}{2}{t^2} \\
 $
On substituting in equation (1)
$
  {t^3} + {\dfrac{\pi }{8}^3} - {t^3} - {\dfrac{{3\pi }}{4}^2}t + \dfrac{{3\pi }}{2}{t^2} - a{\pi ^3} = 0 \\
   \Rightarrow \dfrac{{3\pi }}{2}{t^2} - {\dfrac{{3\pi }}{4}^2}t + {\dfrac{\pi }{8}^3} - a{\pi ^3} = 0 \\
 $
Taking $\pi $as common and multiplying both sides by 2.
$ \Rightarrow 3{t^2} - \dfrac{{3\pi }}{2}t + {\dfrac{\pi }{4}^2} - 2a{\pi ^2} = 0$ …… (2)
Equation (2) is a quadratic equation in variable ‘t’
On comparing with the standard quadratic equation: $a{x^2} + bx + c = 0$
$a = 3,{\text{ }}b = - \dfrac{{3\pi }}{2},{\text{ }}c = {\dfrac{\pi }{4}^2} - 2a{\pi ^2}$
We know, the solution of a quadratic equation exists for $D \geqslant 0$
$D = {b^2} - 4ac$
Here, D is discriminant
Therefore, ${\left( { - \dfrac{{3\pi }}{2}} \right)^2} - 4 \times 3\left( {{{\dfrac{\pi }{4}}^2} - 2a{\pi ^2}} \right) \geqslant 0$
$
   \Rightarrow \dfrac{{9{\pi ^2}}}{4} - 3{\pi ^2} + 24a{\pi ^2} \geqslant 0 \\
   \Rightarrow \dfrac{{9{\pi ^2} - 12{\pi ^2}}}{4} + 24a{\pi ^2} \geqslant 0 \\
   \Rightarrow \dfrac{{ - 3{\pi ^2}}}{4} + 24a{\pi ^2} \geqslant 0 \\
   \Rightarrow 24a{\pi ^2} \geqslant \dfrac{{3{\pi ^2}}}{4} \\
   \Rightarrow 24a \geqslant \dfrac{3}{4} \\
   \Rightarrow a \geqslant \dfrac{3}{{4 \times 24}} \\
   \Rightarrow a \geqslant \dfrac{1}{{32}} \\
 $
Thus, the solution of the given equation exists when $a \geqslant \dfrac{1}{{32}}$.
Step 2: Analysing statement II
The inverse trigonometric identity:
${\sin ^{ - 1}}x + {\cos ^{ - 1}}x = \dfrac{\pi }{2}$ is valid for $x \in \left[ { - 1,1} \right]$
Graph of $y = {\sin ^{ - 1}}x$

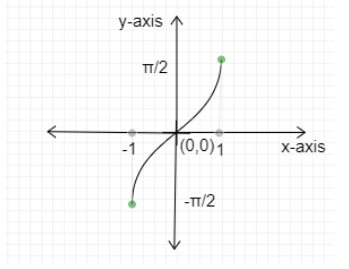
Domain: $\left[ { - 1,1} \right]$
Range: $\left[ { - \dfrac{\pi }{2},\dfrac{\pi }{2}} \right]$
$ \Rightarrow - \dfrac{\pi }{2} \leqslant {\sin ^{ - 1}}x \leqslant \dfrac{\pi }{2}$
Subtracting $\dfrac{\pi }{4}$ to both sides of the inequality.
$
   \Rightarrow - \dfrac{\pi }{2} - \dfrac{\pi }{4} \leqslant \left( {{{\sin }^{ - 1}}x - \dfrac{\pi }{4}} \right) \leqslant \dfrac{\pi }{2} - \dfrac{\pi }{4} \\
   \Rightarrow - \dfrac{{3\pi }}{4} \leqslant \left( {{{\sin }^{ - 1}}x - \dfrac{\pi }{4}} \right) \leqslant \dfrac{\pi }{4} \\
 $
On squaring both sides of the inequality, we get
$0 \leqslant {\left( {{{\sin }^{ - 1}}x - \dfrac{\pi }{4}} \right)^2} \leqslant \dfrac{{9{\pi ^2}}}{{16}}$
In the given statement II, the interval for x is, $x \in \mathbb{R}$ ; but the above equations and expressions are true (or valid) for only $x \in \left[ { - 1,1} \right]$.

On analysis, the statement I comes out to be true but statement II is false. Thus, the correct option is (C).

Note: Following graph will be useful in future reference.
The graph of \[y = {\cos ^{ - 1}}x\] :
Domain: $\left[ { - 1,1} \right]$
Range: $\left[ {0,\pi } \right]$

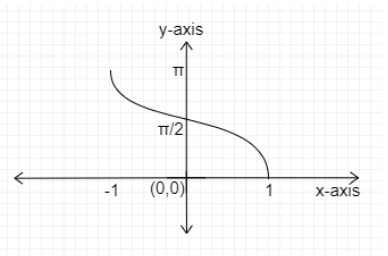
Students might go wrong while squaring the inequality $ - \dfrac{{3\pi }}{4} \leqslant \left( {{{\sin }^{ - 1}}x - \dfrac{\pi }{4}} \right) \leqslant \dfrac{\pi }{4}$.
They might write $\dfrac{{9{\pi ^2}}}{{16}} \leqslant {\left( {{{\sin }^{ - 1}}x - \dfrac{\pi }{4}} \right)^2} \leqslant \dfrac{{{\pi ^2}}}{{16}}$ , this is wrong for the following reasons.
The square of a real number is always greater and equal to zero. This implies $0 \leqslant {\left( {{{\sin }^{ - 1}}x - \dfrac{\pi }{4}} \right)^2}$.
The square of numbers from $\dfrac{{ - 3\pi }}{4}{\text{ to 0}}$ lies between $0{\text{ to }}\dfrac{{9{\pi ^2}}}{{16}}$; and the square of numbers from $0{\text{ to }}\dfrac{\pi }{4}$ lies between $0{\text{ to }}\dfrac{{{\pi ^2}}}{{16}}$; thus, the square of numbers from $\dfrac{{ - 3\pi }}{4}{\text{ to }}\dfrac{\pi }{4}$ lies between $0{\text{ to }}\dfrac{{9{\pi ^2}}}{{16}}$. Therefore the correct inequality is: $0 \leqslant {\left( {{{\sin }^{ - 1}}x - \dfrac{\pi }{4}} \right)^2} \leqslant \dfrac{{9{\pi ^2}}}{{16}}$ .