Question

State whether the given statement is true or false.
Show that the area of rhombus is half the product of the length of its diagonals.
A. TRUE
B. FALSE

Answer 1

Hint: Using the concept of diagonals intersecting at right angles we find the area of rhombus by dividing it into two triangles and adding the areas of two triangles.
* Area of a triangle is half the product of base and height of the triangle.

Complete step-by-step answer:
We draw a figure of a rhombus \[ABCD\] having diagonals \[AC, BD\] which bisect at the point \[O\].
                              

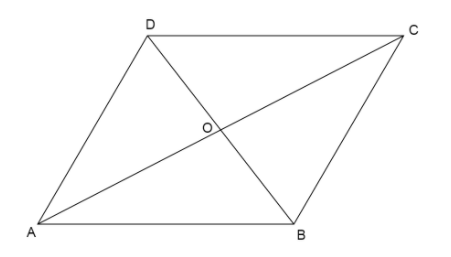
We know a rhombus is a quadrilateral having opposite sides equal and parallel and the diagonals of rhombus intersect at right angles.
So, we can write \[BO \bot AC,DO \bot AC\]
Now we can break the area of the rhombus \[ABCD\] as the sum of the area of triangle \[ABC\] and triangle \[ADC\].
Also, we know in the triangle \[ABC\], the base is \[AC\] and the height is \[BO\].
Similarly, we know in the triangle \[ADC\], the base is \[AC\] and the height is \[DO\].
From the formula of area of a triangle we can write Area \[ = \dfrac{1}{2}\] base \[ \times \]height.
Area of triangle \[ABC = \dfrac{1}{2} \times AC \times BO\]
Area of triangle \[ADC = \dfrac{1}{2} \times AC \times DO\]
Now to calculate the area of rhombus \[ABCD = \]Area of triangle \[ABC + \]Area of triangle \[ADC\]
Substituting the values of area of triangles in the formula
Area of rhombus \[ABCD = \dfrac{1}{2} \times AC \times BO + \dfrac{1}{2} \times AC \times DO\]
Now we take \[\dfrac{1}{2} \times AC\] common and write
\[ \Rightarrow \]Area of rhombus \[ABCD = \dfrac{1}{2} \times AC(BO + DO)\]
Now we write \[BO + DO = BD\]
\[ \Rightarrow \]Area of rhombus \[ABCD = \dfrac{1}{2} \times AC \times (BD)\]
So, the area of the rhombus is half the product of its diagonals.
Therefore, the statement given in the question is TRUE.

So, the correct answer is “Option A”.

Note: Students many times make the mistake of assuming diagonals equal which only happens in a special case of rhombus having all sides equal which makes a rhombus a square.