Question

State whether the given statement is true or false:
Two line segments may intersect at a point which is not the end-point of either of the two segments containing it.

Answer 1

Hint: Two intersecting line segments can intersect each other either at one of the line’s end points, end points of both the intersecting lines or some other interior point. Form different cases for each of them and analyze each case with diagrams.

Complete step by step answer:
If we consider different cases for two intersecting line segments:
Case 1:

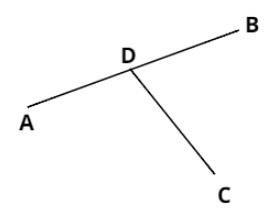
In the above figure, we can clearly see the two line segments are intersecting at point D. And this point is also the end-point of line segment CD.
Case 2:

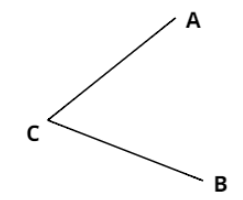
In this figure, line segments AC and BC are intersecting at point C. And this point is the end-point of both AC and BC
Case 3:

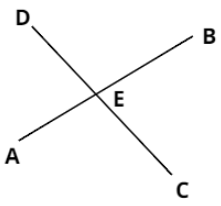
But in this figure, we can see that both the line segments AB and CD are intersecting at point E which is neither the end-point of AB nor the end-point of CD.
Hence, although the first two cases aren’t satisfying the condition given in the question, the third case is perfect with it.

Thus we can say that two line segments may intersect at a point which is not the end-point of either of the two segments containing it. And the statement is true.

Note: Line segments have specific endpoints, that’s why we can solve the above problem for them. Any arbitrary straight line, on the other hand, doesn’t have end points. Two of these lines always intersect each other if they are not parallel. And considering the intersection at end points is ambiguous because they don’t have any defined end points.