Question

State whether the following statement is Right or Wrong;-
“The diagonals of the four-sided quadrilateral known as ‘trapezium’ bisect each other”
(a) Right
(b) Neither Right nor Wrong
(c) Wrong
(d) Cannot determined

Answer 1

Hint: Here, we are going to assume the triangles (having two sides similar) are congruent formed inside the trapezium after drawing the diagonals joining with opposite interior angles and then relating it with side – angle – side theorem contradicting it with real time diagram, the given statement can be easily proven.

Complete step-by-step answer:
A trapezium is a quadrilateral whose opposite sides are parallel and the other corresponding opposite sides intersect at a certain distinct.
From figure above,
First of all let’s talk about the triangles created in the trapezium when two lines (say, diagonal/s) are connected at two different distinct opposite points from each other.
Construction: Draw the diagonals of the trapezium, so that there is a formation of triangles (that is isosceles, where two sides are equal).

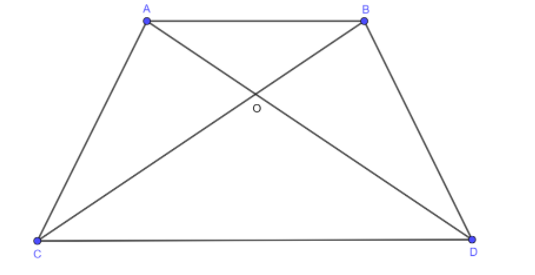
Proof: Now, just assume that the diagonals of the trapezium $ACDB$ drawn , bisect each other at point\[O\], as a result the four different triangles are formed out of which two triangles are isosceles – type triangles.
Since , assuming the diagonals bisecting each other at point \[O\]; the congruent corresponding sides of the trapezium that is sides of the triangles (up and down) respectively with the inside angles that are formed by the triangle and side of the trapezium, that makes the triangles congruent that is equal by the theorem studied in the previous standard called as ‘side – angle - side theorem’ which says that the corresponding sides of the two adjacent angles formed seems to be equal.
But, in practical terms (compared to the figure) the above theorem contradicts because the respective bases of the triangles that are upper and lower sides of the trapezium are obviously not equal.
 Therefore, triangles cannot be similar!
Hence, our proof contains paradox as per as the given statement is concerned.
$ \Rightarrow $The diagonals in the trapezium cannot be bisected.
$\therefore $As a result, option (c) is correct.
So, the correct answer is “Option C”.

Note: While solving the solution or proof to prove the statement remember that diagonals in the trapezium may be similar in length but they cannot be intersected at the midpoint of the trapezium (as per theorem of midpoint studied in earlier classes) respectively.