Question

State whether the following are true or false. Justify your answer.
$\sec A=\dfrac{12}{5}$ for some value of angle A.

Answer 1

Hint: At first use the $\sec A=\dfrac{1}{\cos A}$, then rewrite the statement as $\cos A=\dfrac{5}{12}$. Then use the fact that $\cos \theta $ represents the side adjacent to angle $\theta $ by the hypotenuse or longest side of the triangle which is not possible.

Complete step-by-step answer:
In the question we are asked a statement which is $\sec A=\dfrac{12}{5}$ is either true or false.
In the question value of $\sec A$ is given so we know an identity that $\sec A=\dfrac{1}{\cos A}$ so, if $\sec A=\dfrac{12}{5}$ then we can say that $\cos A=\dfrac{5}{12}$. So, if we prove that the statement $\cos A=\dfrac{5}{12}$ for a value is possible then our work is done.
Before proceeding let us know briefly about cosine function.
In mathematics, the cosine is a trigonometric function of an angle. The cosine of an acute in the context of a right-angled triangle for the specified angle is the ratio of the length of the side that is adjacent to that angle to the length of the longest side of the triangle.
Now, let’s define the cosine function of an acute angle $\alpha $, at first start with a right angle triangle that contains an angle of measure A in the $\Delta ABC$ is angle of interest.

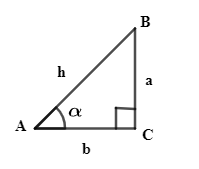
The three sides of the triangle are named as follows:
The opposite is the side opposite to angle of interest as a.
The hypotenuse is side opposite to right angle as h.
The adjacent side is the remaining side in this case side as b.
So, we can represent $\cos \left( \alpha \right)=\dfrac{\text{adjacent}}{\text{hypotenuse}}$
As, we know that adjacent is always less than hypotenuse and it is given that
$\cos A=\dfrac{5}{12}$ which is possible. Hence, the given statement is true.
So, the statement is true.

Note: We can directly say that the statement is true or false by telling the fact that the range of $\sec \theta $ is less than or equal to $-1$ and greater than or equal to 1 which it satisfies.