Question

State true or false:
Two lines perpendicular to the same line are perpendicular to each other:
(A) True
(B) False

Answer 1

Hint: Two lines are said to be perpendicular to each other if an angle ofis formed between them. If two lines are perpendicular to the same line a figure will be formed

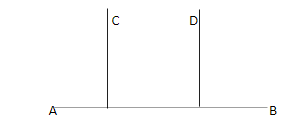
But these two lines do not seem to be perpendicular to each other. Many lines can be perpendicular to the same line. But those are perpendicular to each other that’s not necessary. We can apply the concept of interior alternate angles, corresponding angles. Alternate angles are between the two lines intersected by the transversal they form a Z shape. When two lines are crossed by another line (which is called transversal), the angles in matching corners are called corresponding angles.

Complete step-by-step answer:
Step1: To prove this we may take any figure in which two lines are perpendicular to each other
Let us take a figure in which line AG is perpendicular to FE and line BH is perpendicular to FE

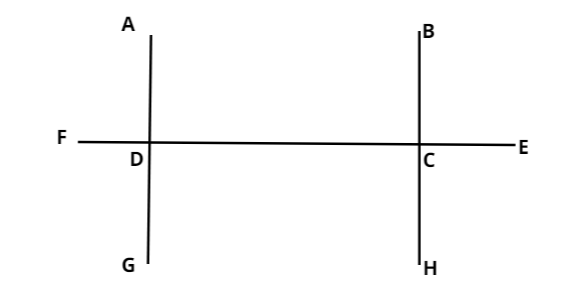
Both the lines are perpendicular to the same line
Step2: From the given figure
$\angle ADC = \angle BCE$$ = {90^ \circ }$ (But these are corresponding angles)
$\angle ADC = \angle DCH = {90^ \circ }$ (But these are interior - alternate angles)
This can only be possible when the line $AG$ is parallel to $BH$. Hence these lines are parallel not perpendicular

Hence option (B) is correct answer statement is false

Note: We can here also prove the lines parallel by:
The sum of co-interior angles are. They lies on the same side of transversal between the two lines
In the above figure the pair of angles that form co-interior angles are $\angle ADC$ and $\angle BCD$
$\angle ADC + \angle BCD = 180$(Sum of co-interior angles are equal)
This can only be possible when lines are parallel then the sum of co-interior angles between them are supplementary.
Hence by this also it proves that lines are not perpendicular they are parallel