Question

State true or false
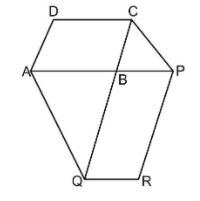
The side $AB$ of a parallelogram $ABCD$ is produced to any point $P$. A line through $A$ and parallel to $CP$ meets $CB$ produced at $Q$ and then parallelogram $PBQR$ is completed. Then ${\text{ar}}\left( {ABCD} \right) = {\text{ar}}\left( {PBQR} \right)$.

A. True
B. False

Answer 1

Hint: Use the concept of a triangle and use the formula for calculating the area of the triangle based on the type of triangle is given. In Euclidean geometry, the non- col-linear points determine a unique triangle.

Complete step-by-step solution:
A triangle is also defined as a closed figure with three edges and three angles and the alternative definition of the triangle is that a triangle is a polygon consisting of three-line segments.
Triangles can be classified according to the lengths of their sides. The sum of three interior angles is always $180^\circ $.
Here, Join the edges $AC$ and $PQ$. $AQ$ is the same base on which both the triangles $ACQ$ and $APQ$ lies.
It can be observed from the given figure that,
${\text{ar}}\left( {\Delta ACQ} \right) = {\text{ar}}\left( {\Delta APQ} \right)$…………..… (1)
Now, subtract the area of the triangle $ABQ$ from both the sides of equation (1). We get,
${\text{area}}\left( {\Delta ABC} \right) = {\text{area}}\left( {QBP} \right)$...............(2)
It is known from the property of parallelogram that diagonal divides a parallelogram in the two triangles of equal area. Here, $AC$ and $QP$ are the two diagonal of the parallelograms $ABCD$ and $PBQR$ respectively. Thus,
The area of \[\Delta ABC\] is equal to the half of the area of the parallelogram $ABCD$.
\[{\text{ar}}\left( {\Delta ABC} \right) = \dfrac{1}{2}{\text{ar}}\left( {ABCD} \right)\] ………………….(3)
And, the area of $\Delta QBP$ is equal to the half of the area of the parallelogram $PBQR$.
${\text{ar}}\left( {\Delta QBP} \right) = \dfrac{1}{2}{\text{ar}}\left( {PBQR} \right)$ …………………..(4)
It can be observed that the area of parallelogram $ABCD$ equals to the area of parallelogram $PBQR$ by using equation (2).
\[{\text{ar}}\left( {ABCD} \right) = {\text{ar}}\left( {PBQR} \right)\].

Hence, the given statement is true.

Note: Properties of parallelogram are
Both pairs of the opposite sides are parallel
Both pairs of the opposite sides are congruent
One pair of opposite sides are congruent
Diagonals bisect each other