Question

State true or false:
\[{\sin ^2}A + {\cos ^2}A = 1\]

Answer 1

Hint: Here we will first draw the right angled triangle \[ABC\]. Then we will find the value of \[\sin A\] and \[\cos A\] using the trigonometric ratios. We will find the square of \[\sin A\] and \[\cos A\] and then we will find their sum. We will use the Pythagoras theorem to simplify it further. If we will get the value as 1 after simplification then the above identity will be true otherwise false.

Complete step-by-step answer:
We have to check whether the given identity \[{\sin ^2}A + {\cos ^2}A = 1\] is true or false.
First, we will draw a right angled triangle \[ABC\]

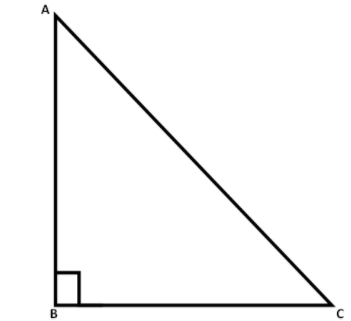
We will first find the value of \[\sin A\] using the trigonometric ratios.
We know that, \[\sin A = \dfrac{P}{H}\] , where \[P\] is perpendicular and \[H\] is hypotenuse.
From the right angled triangle, we have the hypotenuse \[AC\] and the perpendicular \[AB\]. Substituting these values here, we get
\[ \Rightarrow \sin A = \dfrac{{AB}}{{AC}}\]
Squaring both sides, we get
\[ \Rightarrow {\sin ^2}A = {\left( {\dfrac{{AB}}{{AC}}} \right)^2} = \dfrac{{A{B^2}}}{{A{C^2}}}\] ……… \[\left( 1 \right)\]
We will now find the value of \[\cos A\] using the trigonometric ratios.
We know that \[\cos A = \dfrac{B}{H}\], where \[B\] is base and \[H\] is hypotenuse.
From the right angled triangle, we have the hypotenuse \[AC\] and the base \[BC\]. Substituting these values here, we get
\[ \Rightarrow \cos A = \dfrac{{BC}}{{AC}}\]
Squaring both sides, we get
\[ \Rightarrow {\cos ^2}A = {\left( {\dfrac{{BC}}{{AC}}} \right)^2} = \dfrac{{B{C^2}}}{{A{C^2}}}\] ……… \[\left( 2 \right)\]
Now, We will add equation \[\left( 1 \right)\] and equation \[\left( 2 \right)\].
\[ \Rightarrow {\sin ^2}A + {\cos ^2}A = \dfrac{{A{B^2}}}{{A{C^2}}} + \dfrac{{B{C^2}}}{{A{C^2}}}\]
Simplifying the terms, we get
\[ \Rightarrow {\sin ^2}A + {\cos ^2}A = \dfrac{{A{B^2} + B{C^2}}}{{A{C^2}}}\]
Using Pythagoras theorem for this right angled triangle here, we get
\[ \Rightarrow {\sin ^2}A + {\cos ^2}A = \dfrac{{A{C^2}}}{{A{C^2}}} = 1\]
Hence, the given identity is correct or the given statement is true.

Note: We have used trigonometric ratios here to prove the given identity. We need to keep in mind that trigonometric ratios and trigonometric identities are different. Trigonometric identities means the formula which involves trigonometric functions and trigonometric ratios means the formula which shows the relation between angles and length of the right angled triangle.