Question

State True or False.
Points \[M\] and \[N\] are taken on the diagonal \[AC\] of a parallelogram \[ABCD\] such that \[AM = CN\], then \[BMDN\] is a parallelogram
A. TRUE
B. FALSE

Answer 1

Hint: We prove this statement is true or false by using the property that diagonals of a parallelogram bisect each other.
* A parallelogram is a quadrilateral having opposite sides parallel and opposite angles equal.
* Diagonals of a parallelogram bisect each other.

Complete step-by-step answer:
First we draw a diagram of a parallelogram \[ABCD\] having diagonals \[AC\] and \[BD\] and two points \[M\] and \[N\] lie on \[AC\].
                     

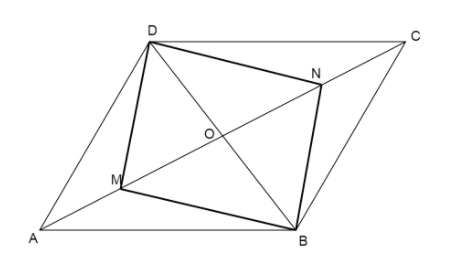
Since, \[ABCD\] is a parallelogram, so its diagonals must bisect each other at point \[O\] .
Therefore, the length \[AO = OC\] and the length \[OB = OD\]
Now we are given two points on the diagonal \[AC\] such that \[AM = CN\].
Subtract \[AM = CN\] from \[AO = OC\]
\[
   \Rightarrow AO - AM = OC - CN \\
   \Rightarrow OM = ON \\
 \]
So, now we look at the quadrilateral \[BMDN\] which has one of its diagonal \[BD\] and the other diagonal as \[MN\].
Since we know the lengths \[OM = ON,OB = OD\], so we can say the diagonals \[BD,MN\] bisect each other at point \[O\].
Therefore, quadrilateral \[BMDN\] is a parallelogram.
So, the statement given in the question is TRUE.

So, the correct answer is “Option A”.

Additional Information:
* A parallelogram has sum of all its four angles equal to \[{360^ \circ }\]
* Area of a parallelogram is always the product of its base and height.
* Each diagonal bisects the triangle into two congruent triangles.
* Alternate interior angles of a parallelogram are always equal.

Note: Students many times make mistake of assuming the length of the diagonals equal so after bisecting all the four parts of diagonals become equal which is wrong because diagonals are not always equal in length, they bisect each other which means the original length of one diagonal gets divided into two equal halves.