Question

State true or false.
If two parallel lines are intersected by a transversal, then the interior angles on the same side of the transversal are supplementary.
A. TRUE
B. FALSE

Answer 1

Hint: Here we use the concept that corresponding angles are equal when a set of parallel lines are cut by a transversal and then we have one of the interior angles and the other interior angle is supplementary to one of the corresponding angles.
* Alternate interior angles are the angles which lie on the inside of the parallel lines but on the same side of the transversal.

Complete step-by-step answer:
Here we draw two parallel lines l and m intersected by a transversal p.
               

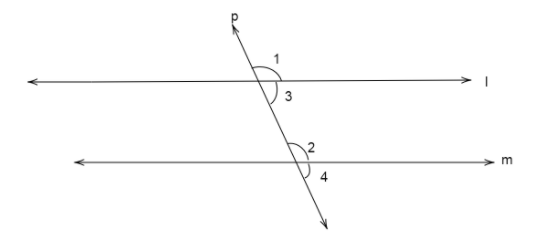
Here the set or corresponding angles are \[\angle 1\] and \[\angle 2\] and the interior angles are \[\angle 3\] and \[\angle 2\]
Since we know when two parallel lines are cut by a transversal then the set of corresponding angles formed are equal to each other.
Therefore, \[\angle 1 = \angle 2\]
Now since we can see the set of angles are supplementary as they lie on a straight line p and are cut by line l , so we can write \[\angle 1 + \angle 3 = {180^ \circ }\].
Therefore, the value of \[\angle 3 = {180^ \circ } - \angle 1\] … (i)
Replacing the value of \[\angle 1 = \angle 2\] in equation (i) we get
\[\angle 3 = {180^ \circ } - \angle 2\]
Shifting the angles to one side
\[\angle 3 + \angle 2 = {180^ \circ }\]
The above equation gives us the sum of interior angles equal to \[{180^ \circ }\] which means the angles are supplementary.
Therefore, the statement given in the question is TRUE.

So, the correct answer is “Option A”.

Note: Students many times make the mistake of writing and assuming alternate interior angles in this question but they should keep in mind that alternate interior angles are the interior angles on the opposite sides of the transversal whereas the interior angles are on the same side of the transversal.