Question

State true or false.
If a number of circles touch a given line segment $PQ$ at mid-point $A$, then their centres lie on the perpendicular bisector of $PQ$.
A) True
B) False

Answer 1

Hint: In this question, we are given a statement and we have to tell whether it is true or false. Draw a circle with any radius and then draw a line segment PQ passing through it at point A, such that $AP = AQ$ (it is given that A is the midpoint of PQ). Draw as many circles with tangent $PQ$, touching the circles at $A$. Then take two right angled triangles with AP and AQ as base and prove them congruent. Then it will show that the center of the circle will always lie on the perpendicular bisector.

Complete step-by-step solution:
We are given a statement here and we have to tell whether it is true or false. We will try to prove the statement true or false.
Draw a circle with center D of any radius. Then, draw a tangent $PQ$ touching the circle at point $A$, such that $AP = AQ$ (it is given that A is the midpoint of PQ). Now, draw as many circles as you can with tangent $PQ$, touching the circles at $A$.

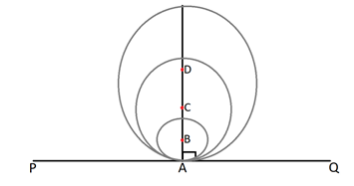
Now, join the centres with the point $A$ (point of contact of tangent). They will make an angle of $90^\circ $ as the radius is perpendicular to the tangent at the point of contact. Join D with P and Q.

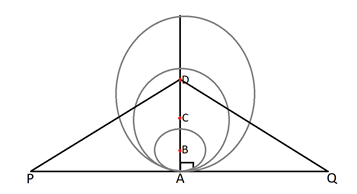
 Now, consider the $\vartriangle DAP$ and $\vartriangle DAQ$.
$ \Rightarrow DA = DA$ (common)
$ \Rightarrow AP = AQ$ (it is given that A is the mid-point of PQ)
$ \Rightarrow \angle DAP = \angle DAQ = 90^\circ $ (radius is perpendicular to the tangent at the point of contact)
Therefore, $\vartriangle DAP \cong \vartriangle DAQ$ (by SAS rule)
Now, we can say that $DP = DQ$ (by corresponding part of congruent triangles)
In the similar way $\vartriangle CAP \cong \vartriangle CAQ$ and $\vartriangle BAP \cong \vartriangle BAQ$.
Therefore, $CP = CQ$ and $BP = BQ$ (by corresponding part of congruent triangles)
As we can see, DA is the perpendicular bisector of PQ. It shows that the center of all the circles lie on the perpendicular bisector DA.

Hence, the given statement that - If a number of circles touch a given line segment $PQ$ at mid-point $A$, then their centres lie on the perpendicular bisector of $PQ$, is true.

Note: Here, we used congruence and not similarity to prove the required because if two triangles are proved congruent, then they are equal in size and shape, which means that the sides are equal in measure. This was required to prove what is required. On the other hand, similarity just means that the sides are proportional and not equal. This was not required. That is why we used congruence and not similarity.