Question

State true or false:
Angles forming a linear pair are supplementary.
A. True
B. False

Answer 1

Hint: In this question, we need to check if angles forming a linear pair are supplementary or not. For this, we need to prove if angles forming a linear pair form a sum of ${{180}^{\circ }}$ or not. First, we will understand the meaning of linear pairs and then prove their sum to be equal to ${{180}^{\circ }}$ using diagrams.

Complete step-by-step solution
Linear pairs of angles are formed when two lines intersect each other at a single point. The angles are said to be linear if they are adjacent to each other after the intersection of the two lines. Now we need to prove that angles forming a linear pair are supplementary, that is, the sum of angles forming a linear pair is ${{180}^{\circ }}$. Let us draw a diagram to understand the concept clearly. Let AB and CD are two lines that intersect at O.

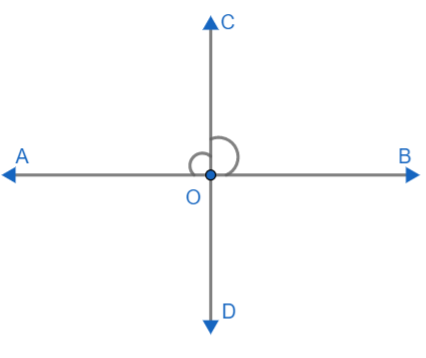
Now, as we can see $\angle AOC\text{ and }\angle BOC$ are adjacent to each other after the intersection of two lines. So, $\angle AOC\text{ and }\angle BOC$ form a linear pair.
From the diagram, we can say that, the sum of $\angle AOC\text{ and }\angle BOC$ is equal to the $\angle AOB$.
Hence, $\angle AOC\text{ and }\angle BOC=\angle AOB$.
Since, $\angle AOB$ is an angle on a line AB and hence, it is a straight angle. Therefore, $\angle AOB={{180}^{\circ }}$.
Now we get, $\angle AOC\text{ and }\angle BOC={{90}^{\circ }}$.
As we can see, the sum of $\angle AOC\text{ and }\angle BOC$ is ${{180}^{\circ }}$ which means these are supplementary angles. They were linear pairs of angles, so we can say that angles forming a linear pair are supplementary.
Hence, the statement is true.
Therefore, option A is the correct answer.

Note: For solving this sum, students should know the meaning of the term linear pair and supplementary angles. Students can get confused between the terms supplementary angle and complementary angle. The angle whose sum is ${{180}^{\circ }}$ is called the supplementary angle and the angle whose sum is ${{90}^{\circ }}$ are called complementary angles. Line CD need not be perpendicular (as shown) to AB. It can intersect AB at any angle.