Question

State true or false: All squares are not parallelograms.
A. true
B. false
C. ambiguous
D. data insufficient

Answer 1

Hint: We first try to explain the concept of squares and parallelograms. We also discuss the relation between them. We use that to find the concept of non-square parallelograms with the help of diagrams which gives the right option for the problem.

Complete step-by-step solution:
A parallelogram can be defined in the form of a quadrilateral which has its opposite sides parallel or equal or both. It has no particular condition of consecutive sides being congruent to each other. If the consecutive sides of parallelogram are equal then it becomes a particular form of parallelogram which is rhombus.
Now when we take a square, we can define it in the form of a rhombus where a rhombus converts into a square with its all angles being equal to each other.
This means the angle of the square becomes equal to $\dfrac{\pi }{2}$.

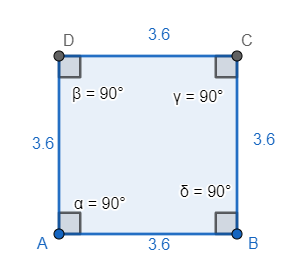
Therefore, square is a particular form of parallelogram. The above picture is of a square as well as a parallelogram. We can say that all squares are parallelograms but all parallelograms aren’t squares.

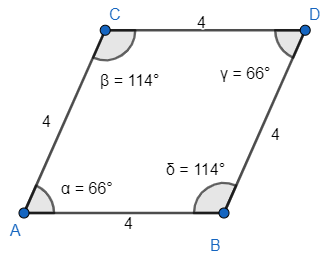
This is an image of parallelogram but it is not a square as its two consecutive angles aren’t congruent. These are called non-square parallelograms. The correct option is B.

Note: To put it simply a parallelogram is generally created by parallel lines, which may be square in some particular cases. The concept of congruent and regular is different. The concept of irregular quadrilateral comes from congruent sides and angles being not equal. This is different from being congruent.