Question

State the whether given statement is true or false
ABCD is a parallelogram. AB produced E so that \[BE = AB\] then, ED bisects BC.
 A) True
B) False

Answer 1

Hint: First we will construct a parallelogram ABCD with AB produced at E and then use the congruence of two triangles to check whether ED bisects BC (\[BM = MC\]) or not.

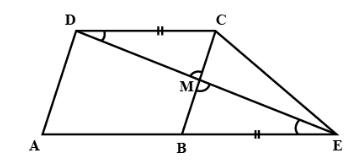
Complete step-by-step answer:
Since we know that ABCD is a parallelogram and the opposite sides of a parallelogram are parallel as well as equal
Therefore,
\[AB = CD\]……………………(1)
Also, it is given that:
\[AB = BE\]………………….(2)
Equating equations 1 and 2 we get:-
\[BE = CD\]……………………..(3)
Now consider \[\Delta CMD\] and \[\Delta BEM\;\]
\[
  BE = CD\;\left( {from{\text{ 3}}} \right){\text{ }}\;{\text{ }}\; \\
  \angle CDM = \angle BEM(\because CD|{\text{ | }}AE{\text{ and alternate interior angles}})\; \\
  \angle DCM = \angle EMB(\because CD|{\text{ | }}AE{\text{ and alternate interior angles}}) \\
 \]
Hence,
By ASA criterion of congruence of triangles
\[\Delta CMD \cong \Delta BEM\]
Therefore,
\[BM = CM\left( {{\text{by correponding parts of congruent triangles}}} \right)\]
Hence ED bisects BC
Therefore the given statement is true.
Hence option A is correct.

Additional Information:
Two triangles can be congruent by following congruence criterions:-
SSS criterion: - In SSS congruence criterion the two triangles are congruent if all the sides of a triangle are equal to the corresponding sides of another triangle.
ASA criterion: - In ASA congruence criterion the two triangles are congruence if two angles and the side containing them of a triangle are equal to the corresponding angles and side of another triangle.
SAS criterion: - In SAS congruence criterion the two triangles are congruent if two sides and an angle between them of a triangle are equal to the corresponding sides and angle of another triangle.
AAA criterion: - In AAA congruence criterion the two triangles are congruent if all the angles of a triangle are equal to the corresponding angles of another triangle.

Note: Students should keep in two important properties of the parallelogram used:
1) Opposite sides of the parallelogram are equal
2) Opposite sides of the parallelogram are parallel.
Also, if two triangles are congruent then
All the corresponding angles and sides of those two triangles are equal by corresponding parts of congruent triangles.