Question

State the numerical value of the frequency of oscillation of a second’s pendulum? Does it depend on the amplitude of the oscillation?

Answer 1

Hint: We all know that the time period of the pendulum the amount of time a pendulum takes to come to the initial position when starting from the same initial mean position. While completing a 1-time period, the pendulum goes to two extreme positions also.

Formula Used:
The formula for calculating the frequency is of the pendulum is:
$f = \dfrac{1}{T}$

Complete step by step answer:
The formula for calculating the frequency is:
$f = \dfrac{1}{T}$
Put the value of time period (T) as 2 seconds in the above equation.
$\begin{array}{c}
f = \dfrac{1}{{2\,{\rm{s}}}}\\
 = 0.5\,
\end{array}$
We can refer to the below figure for the diagram of the pendulum which is the length l of the pendulum and the mass of the bob is m.

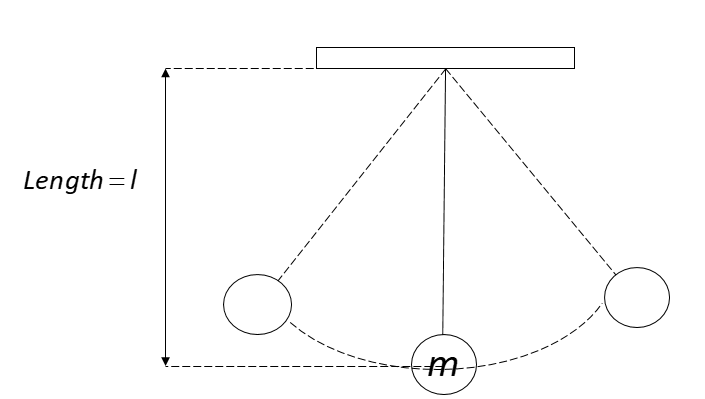
The frequency of the oscillation of a second’s pendulum depends on the time period of the oscillation. The time period further depends on the length of the pendulum and the acceleration due to gravity. Hence, the oscillation of a second’s pendulum is independent of the amplitude of the oscillation.

Additional Information:
The time period of the pendulum is also constant if there is no air drag or atmospheric friction. The time period of a pendulum in the moon will increase as the value of acceleration due to gravity g is less in the moon.

Note:
The effective length of the second’s pendulum, at a place where the value of acceleration due to gravity is g=9.8 m/$s^2$ (the average value), is nearly one meter. Here the string is considered as massless and only the mass of the bob is considered.