Question

State Euclid’s fifth postulate. Using the same write the pairs of angles, having the sum less than \[180^\circ \]. (From the figure given)

Answer 1

Hint: Write Euclid’s postulate as it is described by Euclid in the first place. Then use the facts given in the postulate to analyze the figure and find the solution.

Complete step by step solution: Euclid’s fifth postulate:
If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles i.e., 180∘, then the two straight lines, if produced indefinitely meet on that side on which sum of angles is less than two right angles.
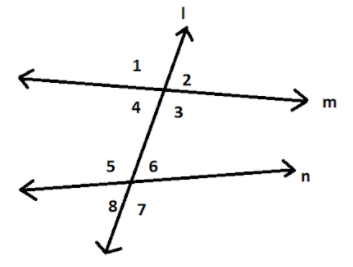
So, here according to this image it is given, there are two given lines m and n, and the line l is intersecting these two lines.
Now, if we check the right side of the line l, we can see 4 angles, 2, 3, 6 and 7.
So, as per Euclid’s fifth postulate, if produced indefinitely meet on that side on which sum of angles is less than two right angles. So, we get,

\[\angle 3 + \angle 6 < 180^\circ \].

Note: The fifth postulate is also known as the Parallel Postulate because it can be used to prove properties of parallel lines.
In a plane, given a line and a point not on the line, there are exactly three possibilities with regard to the number of lines through the point:
1) There is exactly one line parallel to the given line;
2) There is no line parallel to the given line;
3) There is more than one line parallel to the given line.