Answer
416.1k+ views
Hint- In this question, we have to prove the ratio of areas of two similar triangles is always equal to the square of its corresponding sides. Now to solve this question one should know about the basic properties of similarity of triangles. The basic is that the angles in similar triangles are equal. Then second is that the ratio of corresponding sides of a similar triangle is also equal. These are the properties used in the question also one will notice that later on the triangle is divided into two parts to be able to prove the theorem.
Complete step-by-step answer:
Area theorem, the ratio of areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.
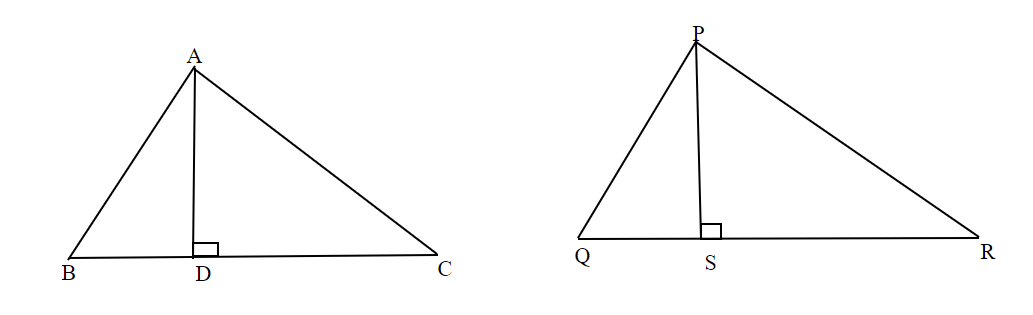
Given,$\vartriangle ABD \sim \vartriangle PQR$
$
\therefore \angle A = \angle P,\angle B = \angle Q,\angle C = \angle R \\
\dfrac{{AB}}{{PQ}} = \dfrac{{BC}}{{QR}} = \dfrac{{CA}}{{PR}}{\text{ }}......\left( 1 \right) \\
$
The ratio of $\vartriangle ABD$and $\vartriangle PQR$ is given as,
$
\dfrac{{ar\left( {\vartriangle ABC} \right)}}{{ar\left( {\vartriangle PQR} \right)}} = \dfrac{{\dfrac{1}{2} \times BC \times AD}}{{\dfrac{1}{2} \times QR \times PS}} \\
\dfrac{{ar\left( {\vartriangle ABC} \right)}}{{ar\left( {PQR} \right)}} = \dfrac{{BC}}{{QR}} = \dfrac{{AD}}{{PS}}{\text{ }}......\left( 2 \right) \\
$
In $\vartriangle ABD$ and $\vartriangle PQS$
$
\angle B = \angle Q{\text{ }}\left[ {Given} \right] \\
\angle ABD = \angle PSQ{\text{ }}\left[ {Each{\text{ }}{{90}^ \circ }} \right] \\
\therefore \vartriangle ABD \sim \vartriangle PQS{\text{ }}\left[ {AA{\text{ similarity}}} \right] \\
$
$ \Rightarrow \dfrac{{AD}}{{PS}} = \dfrac{{AB}}{{PQ}} = \dfrac{{BD}}{{QS}}{\text{ }}.....\left( 3 \right){\text{ }}\left[ {Corresponding{\text{ sides are propotional}}} \right]$
From (1) and (3), we get
$\dfrac{{AB}}{{PQ}} = \dfrac{{BC}}{{QR}} = \dfrac{{CA}}{{PR}} = \dfrac{{AD}}{{PS}}$
$\dfrac{{BC}}{{QR}} = \dfrac{{AD}}{{PS}}$
From (2) and (4), we get
$
\dfrac{{ar\left( {\vartriangle ABC} \right)}}{{ar\left( {\vartriangle PQR} \right)}} = \dfrac{{BC}}{{QR}} \times \dfrac{{BC}}{{QR}} = \dfrac{{B{C^2}}}{{Q{R^2}}} \\
\therefore \dfrac{{ar\left( {ABC} \right)}}{{ar\left( {PQR} \right)}} = \dfrac{{A{B^2}}}{{P{Q^2}}} = \dfrac{{B{C^2}}}{{Q{R^2}}} = \dfrac{{C{A^2}}}{{P{R^2}}} \\
\\
$
Using (1), Hence proved.
Note- In this question it should be noted that we use the basic properties of similarity in the triangles in the question. But we should know that we have to prove that the ratio of areas of the triangle is equal to the square of its corresponding sides. By keeping this in mind we should know the basic properties of similarity in triangles like angles in similar triangles are equal, then the ratio of corresponding sides is equal. Now to make the task easier we should know that the triangle is divided so this will make the question easier to solve. Thus by these steps it will become easy to solve the question.
Complete step-by-step answer:
Area theorem, the ratio of areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.
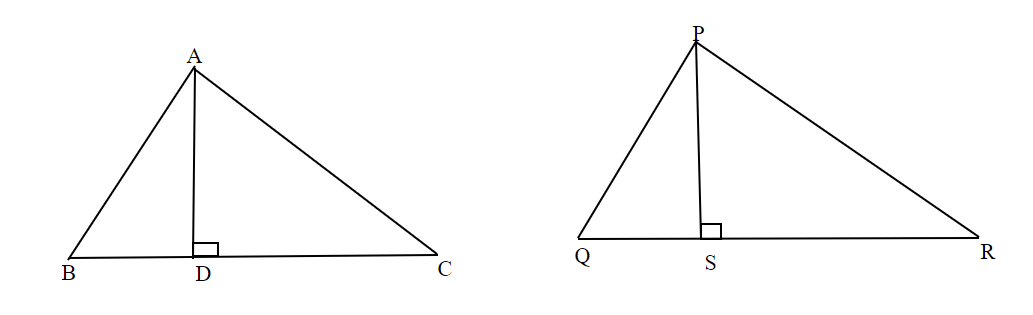
Given,$\vartriangle ABD \sim \vartriangle PQR$
$
\therefore \angle A = \angle P,\angle B = \angle Q,\angle C = \angle R \\
\dfrac{{AB}}{{PQ}} = \dfrac{{BC}}{{QR}} = \dfrac{{CA}}{{PR}}{\text{ }}......\left( 1 \right) \\
$
The ratio of $\vartriangle ABD$and $\vartriangle PQR$ is given as,
$
\dfrac{{ar\left( {\vartriangle ABC} \right)}}{{ar\left( {\vartriangle PQR} \right)}} = \dfrac{{\dfrac{1}{2} \times BC \times AD}}{{\dfrac{1}{2} \times QR \times PS}} \\
\dfrac{{ar\left( {\vartriangle ABC} \right)}}{{ar\left( {PQR} \right)}} = \dfrac{{BC}}{{QR}} = \dfrac{{AD}}{{PS}}{\text{ }}......\left( 2 \right) \\
$
In $\vartriangle ABD$ and $\vartriangle PQS$
$
\angle B = \angle Q{\text{ }}\left[ {Given} \right] \\
\angle ABD = \angle PSQ{\text{ }}\left[ {Each{\text{ }}{{90}^ \circ }} \right] \\
\therefore \vartriangle ABD \sim \vartriangle PQS{\text{ }}\left[ {AA{\text{ similarity}}} \right] \\
$
$ \Rightarrow \dfrac{{AD}}{{PS}} = \dfrac{{AB}}{{PQ}} = \dfrac{{BD}}{{QS}}{\text{ }}.....\left( 3 \right){\text{ }}\left[ {Corresponding{\text{ sides are propotional}}} \right]$
From (1) and (3), we get
$\dfrac{{AB}}{{PQ}} = \dfrac{{BC}}{{QR}} = \dfrac{{CA}}{{PR}} = \dfrac{{AD}}{{PS}}$
$\dfrac{{BC}}{{QR}} = \dfrac{{AD}}{{PS}}$
From (2) and (4), we get
$
\dfrac{{ar\left( {\vartriangle ABC} \right)}}{{ar\left( {\vartriangle PQR} \right)}} = \dfrac{{BC}}{{QR}} \times \dfrac{{BC}}{{QR}} = \dfrac{{B{C^2}}}{{Q{R^2}}} \\
\therefore \dfrac{{ar\left( {ABC} \right)}}{{ar\left( {PQR} \right)}} = \dfrac{{A{B^2}}}{{P{Q^2}}} = \dfrac{{B{C^2}}}{{Q{R^2}}} = \dfrac{{C{A^2}}}{{P{R^2}}} \\
\\
$
Using (1), Hence proved.
Note- In this question it should be noted that we use the basic properties of similarity in the triangles in the question. But we should know that we have to prove that the ratio of areas of the triangle is equal to the square of its corresponding sides. By keeping this in mind we should know the basic properties of similarity in triangles like angles in similar triangles are equal, then the ratio of corresponding sides is equal. Now to make the task easier we should know that the triangle is divided so this will make the question easier to solve. Thus by these steps it will become easy to solve the question.
Recently Updated Pages
The branch of science which deals with nature and natural class 10 physics CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Define absolute refractive index of a medium

Find out what do the algal bloom and redtides sign class 10 biology CBSE

Prove that the function fleft x right xn is continuous class 12 maths CBSE

Find the values of other five trigonometric functions class 10 maths CBSE

Trending doubts
Difference between Prokaryotic cell and Eukaryotic class 11 biology CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Write an application to the principal requesting five class 10 english CBSE

Difference Between Plant Cell and Animal Cell

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Change the following sentences into negative and interrogative class 10 english CBSE

What organs are located on the left side of your body class 11 biology CBSE

Discuss what these phrases mean to you A a yellow wood class 9 english CBSE

List some examples of Rabi and Kharif crops class 8 biology CBSE



