Question

State and explain the triangle law of vector addition.

Answer 1

Hint: Vector addition is the process of adding two or more vectors together into a vector sum. It is defined as the geometrical sum of two or more vectors. They do not follow any rules and regulations of algebra. There are two laws of vector addition one of which is the triangle law of vector addition and the other is the parallelogram law of vector addition. We are going to see about the triangle law of vector addition in detail.

Complete step-by-step solution:
The triangle law of vector addition says that “Consider two vectors as the two sides of the triangle of the order of same magnitude and the direction, then the third side of the triangle will represent the magnitude and direction of the resultant vector”.

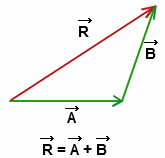
Explanation of the law:
If we have two vectors, \[\vec A\] and \[\vec B\]. We can find the resultant vector as follows. We can refer to the two vectors in the below diagram

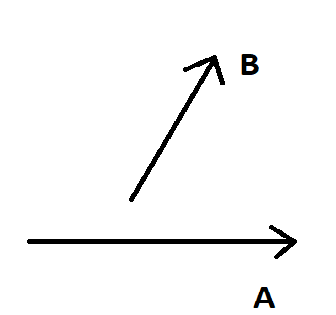
These two vectors \[\vec A\] and \[\vec B\] will both have the same magnitude and direction. If we move \[\vec B\] parallel such that the tail of \[\vec B\] coincides with the head of \[\vec A\].

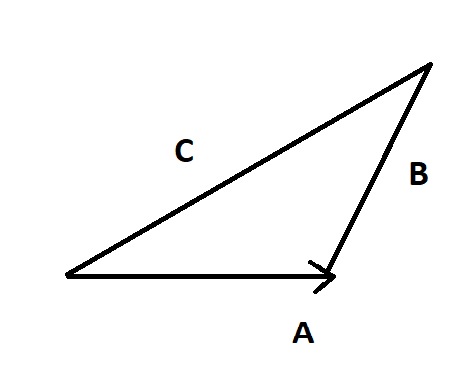
Therefore the vector addition of \[\vec A\] and \[\vec B\] will be the third side that is \[\vec C\]. This is what is known as the triangle law of vector addition.

Note: We should know some basic conditions in vector addition. They are as follows. One is scalars and vectors can never be added. For any two scalars to be added they must be of the same nature and similarly for any two vectors to be added they must have the same nature. The triangle law of vectors can be used in both acute and obtuse angles.