Question

Starting with the same initial conditions, an ideal gas expands from volume \[{{V}_{1}}\]to \[{{V}_{2}}\]in three different ways. The work done by the gas is \[{{W}_{1}}\], if the process is purely isothermal, \[{{W}_{2}}\]is purely isobaric and \[{{W}_{3}}\] if purely adiabatic. Then,
\[\begin{align}
  & A.\,{{W}_{2}}>{{W}_{1}}>{{W}_{3}} \\
 & B.\,{{W}_{2}}>{{W}_{3}}>{{W}_{1}} \\
 & C.\,{{W}_{1}}>{{W}_{2}}>{{W}_{3}} \\
 & D.\,{{W}_{1}}>{{W}_{3}}>{{W}_{2}} \\
\end{align}\]

Answer 1

Hint: Firstly, we will define the thermodynamic process, that is, the isothermal process, adiabatic process and isobaric process. Then, using the graph of pressure versus volume, we will compare the work done by all these three thermodynamic processes.

Complete answer:
Isothermal process – a thermodynamic process in which the temperature of the system remains constant. Isobaric process – a thermodynamic process in which the pressure of the system remains constant. Adiabatic process – a thermodynamic process in which there is no transfer of mass of heat between the system and the surrounding.
The isothermal graph is an exponentially decreasing curve, the isobaric graph is a curve parallel to the x-axis and the adiabatic graph is also an exponentially decreasing curve, mostly a curve that lies below the isothermal curve.

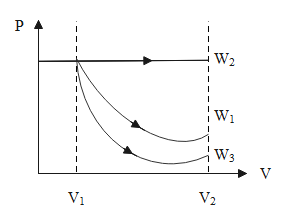
For the same value of the volume, the pressure will be more in the case of the isobaric process, the pressure will be least in the case of the adiabatic process and in the case of the isothermal process, the pressure lies in between. The mathematical representation of the same is, \[{{W}_{2}}>{{W}_{1}}>{{W}_{3}}\].
\[\therefore \] The work done by the isobaric process is more than that of the isothermal process and the work done by the isothermal process is more than that of the adiabatic process.

Thus, option (A) is correct.

Note:
The slope of the pressure versus volume graph gives the value of the work done during the process by the system. As the initial conditions of an ideal gas before expanding were the same for all the processes, thus, the graph of all the processes started from the same point.