Question

Standing waves are set up on strings fixed at both ends. In each case in column-I, l is length of the string, c is the wave speed and f is the wave frequency. Each choice in Column-II lists respectively the number of nodes and antinodes formed on the string .Number of nodes includes the ones formed at the two ends.

Column I	Column II
$l = 0.5m,c = 15m/s,f = 30Hz$	1	2,1
$l = 0.4m,c = 20m/s,f = 50Hz$	2	3,2
$l = 0.6,c = 15m/s,f = 37.5Hz$	3	2,3
$l = 0.5m,c = 25m/s,f = 100Hz$	4	3,4
	5	4,3
	6	5,4

Answer 1

Hint
We need to match both the columns with the correct number of nodes and antinodes. To calculate the number of nodes, we use the formula that gives us n as the number of harmonics. Each harmonic has $n$ number of nodes and $n + 1$ number of antinodes.
$\Rightarrow f = \dfrac{n}{{2l}} \times c$
Here, f is the frequency of the wave,
l is the length of the string ,
c is the wave speed,
n is the number of harmonics produced by a string.

Complete step by step answer
When a string is fixed in one end and another repeatedly oscillates up and down in a regular manner, it creates a wave in the string. At a particular frequency, the wave formed is reflected in the starting end of the string with the same angle, in other words, the wave backtracks its path.
This creates visible observation of a standing wave, this wave appears to be only moving up and down in a fixed number of sets separated by non-moving (fixed) points on the string, called the nodes.
The parts of the string which have the highest displacement (form both crests and troughs) are known as antinodes.
The phenomenon of the standing wave only forms in specific frequencies, each frequency forms a different pattern, known as a harmonic.
For the first harmonic, the number of nodes is 2 (the 2 fixed ends) and 1 antinode which oscillates up and down.
The following diagram shows this-

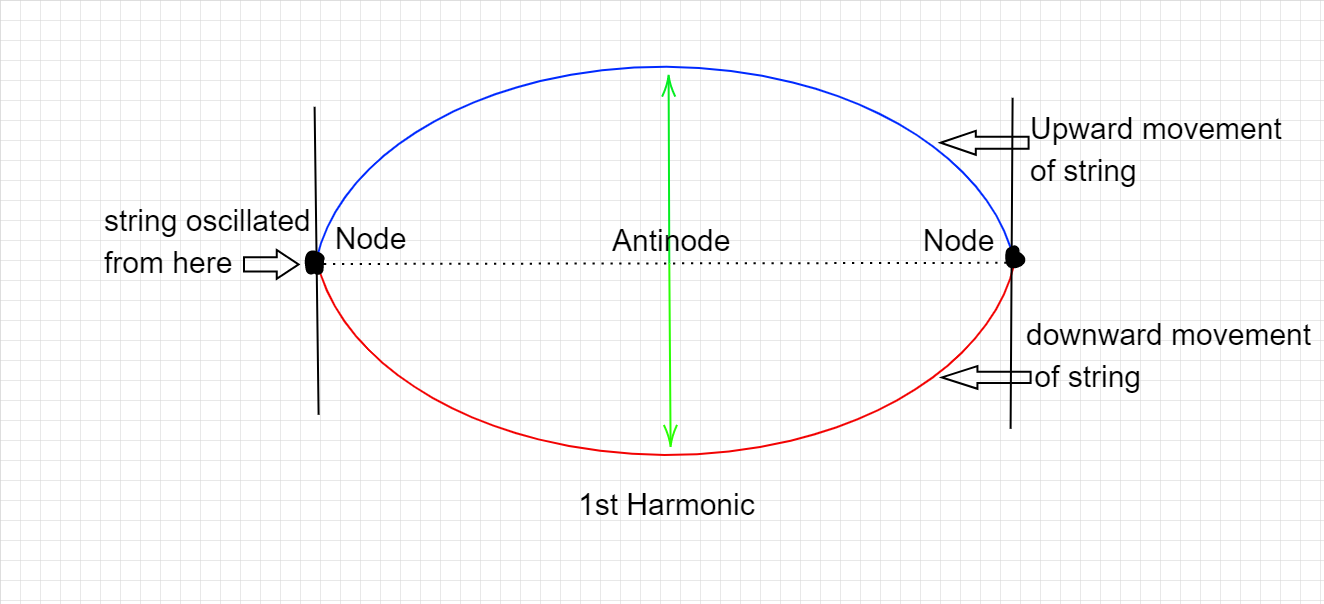
Number of antinodes = Number of harmonics
The formula to calculate antinode is, \[n = \dfrac{{2 \times l \times f}}{c}\]
And, the number of node is given by, $n+1$
Solving the question-
Given, $l = 0.5m,c = 15m/s,f = 30Hz$
$\Rightarrow n = \dfrac{{2 \times 30 \times 0.5}}{{15}}$
$\Rightarrow n = 2$
Number of antinodes$ = 2$
Number of nodes$ = 3$
The correct option is (2).
Given, $l = 0.4m,c = 20m/s,f = 50Hz$
$\Rightarrow n = \dfrac{{2 \times 50 \times 0.4}}{{20}}$
$\Rightarrow n = 2$
Number of antinodes$ = 2$
Number of nodes$ = 3$
The correct option is (2).
Given, $l = 0.6,c = 15m/s,f = 37.5Hz$
$\Rightarrow n = \dfrac{{2 \times 37.5 \times 0.6}}{{15}}$
$\Rightarrow n = 3$
Number of antinodes$ = 3$
Number of nodes$ = 4$
The correct option is (5).
Given, $l = 0.5m,c = 25m/s,f = 100Hz$
$\Rightarrow n = \dfrac{{2 \times 100 \times 0.5}}{{25}}$
$\Rightarrow n = 4$
Number of antinodes$ = 4$
Number of nodes$ = 5$
The correct option is (6).

Note
As the number of nodes is always greater than the number of antinodes, the options with the number of nodes less than antinodes can never be the answer, options (3) and (4) can never be the answer to this question.