Question

Standing waves are produced in \[10m\] long stretched strings. If the string vibrates in 5 segments and wave velocity is \[20m{s^{ - 1}}\] , then its frequency will be
A. \[5Hz\]
B. \[2Hz\]
C. \[10Hz\]
D. \[12Hz\]

Answer 1

Hint: To answer the question, we will build a simple diagram based on the question. The entire length of the string is \[10m\] , and there are five segments, so we will compute the length of one segment and determine the value of $\lambda $ , and then calculate the frequency $(\nu )$ using this $\lambda $ .

Complete answer:
Before we go into the question, let's have a look at what a standing wave is. The combination of two waves flowing in opposite directions, each with the same amplitude and frequency, is known as a standing wave.
Now, let us come to the question;
The wavelength of a stretched string's fundamental vibrational mode is twice the length of the string.

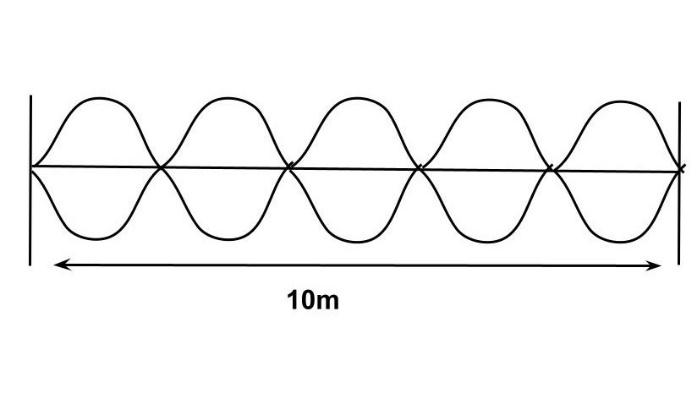
Because the string produces standing waves and vibrates in five parts, it can be shown as
\[\therefore 5\dfrac{\lambda }{2} = 10\]
Therefore, from here we will find value of $\lambda $
\[ \Rightarrow \lambda = 4{\mkern 1mu} m\]
The wave's velocity, \[v\] , is given to us in the question as $v = 20m{s^{ - 1}}$
Hence, the frequency will be \[\nu = \dfrac{v}{\lambda } = \dfrac{{20}}{4} = 5{\mkern 1mu} {s^{ - 1}} = 5{\mkern 1mu} Hz\]
Therefore, the frequency is \[5Hz\]
The correct option is: (A) \[5Hz\]

Note:
It's important to note that standing waves don't just appear out of nowhere. They call for energy to be delivered into a system at a specific frequency. That is, when a system's driving frequency is identical to its natural frequency. Resonance is the term for this situation. Standing waves are invariably linked to resonance.