Question

Standing at \[5m\] apart from a vertical pole of height \[3m\] , Sudha observed a building at the back of the pillar such that the tip of the pillar is in line with the top of the building. If the distance between pillar and building is \[10m\] , estimate the height of the building.

Answer 1

Hint: In order to solve this question, we first need to construct a figure according to the information given in the question. After that, by applying the properties of the geometry and based on the angles formed, we can solve the question.
Formula used: The angle formed at the point \[S\] by both the triangles is the common angle and hence is equal for both the triangles. And we get
 \[\left| \!{\underline {\,
  PSQ \,}} \right. =\left| \!{\underline {\,
  BSA \,}} \right. \]
If two angles are equal then their tangents are also equal.
The tangent function of an angle in a triangle is given by
 \[\tan \left( angle \right)=\dfrac{Perpendicular}{base}\]

Complete step by step solution:
In order to solve this question, let us first construct the figure
The figure for the given information can be drawn as

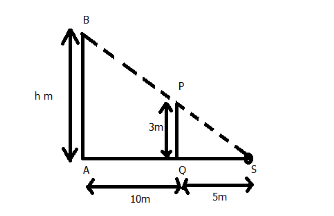
As we can see, in triangle PQS,
 \[
 PQ=3m \\
QS=5m \;
\]
This implies
 \[\tan \left( PSQ \right)=\dfrac{PQ}{QS}=\dfrac{3}{5}\]
Now in triangle, BAS,
 \[
 BA=\left( h \right)m \\
AS=15m \;
\]
Therefore,
 \[\tan \left( BSA \right)=\dfrac{BS}{AS}=\dfrac{h}{15}\]
Now as the both angles are common angles, i.e.,
 \[
 \left| \!{\underline {\,
  PSQ \,}} \right. =\left| \!{\underline {\,
  BSA \,}} \right. \\
\Rightarrow \tan \left( PSQ \right)=\tan \left( BSA \right) \;
\]
Thus, putting the values of both in the equation
 \[
 \dfrac{3}{5}=\dfrac{h}{15} \\
\Rightarrow \dfrac{3\times 15}{5}=h \\
\Rightarrow 9=h \;
\]
Therefore, the height of the building is \[9\] meters.
So, the correct answer is “ \[9\] meters”.

Note: Since the observer sudha has been considered as a point object, therefore, we can consider the triangles as in the figure, however, if Sudha’s height were to be considered, then the question would have been solved in a different way.