
What is standard atmospheric pressure?
Answer
487.8k+ views
Hint: Atmospheric pressure also known as the barometric pressure is defined as the force exerted by the air column on per unit area. Atmospheric pressure can be measured from a barometer where the mercury reading gives the accurate reading. We are going to find the standard atmospheric pressure using a barometer.
Complete answer:
Standard atmospheric pressure refers to the atmospheric pressure exerted by air on any unit surface area of substance. Let us find the atmospheric pressure using mercury barometer.
We can measure the atmospheric pressure at a point using a simple instrument called mercury barometer.
A long glass tube, closed at one end, is filled with mercury. It is then inverted over a trough containing mercury. Mercury in the tube slides down, till it becomes stable at a level. Due to this, the level of the mercury rises in the trough. When the level of the mercury becomes stable in the tube, we say that the pressure exerted by mercury is the same as the atmospheric pressure.
At sea level the mercury column in the barometer tube has a height of about above the mercury level in the trough.
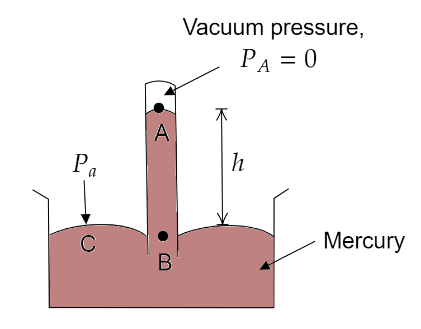
Let us consider two points B and C at the same horizontal level as shown in the above figure. As they are at the same horizontal level, the same pressure acts at these points.
$ \Rightarrow {P_C} = {P_B} = {P_a}$ (atmospheric pressure)
But according to the expression for absolute pressure,
${P_B} = {P_A} + \rho gh$
Where, $\rho = $ density of mercury and $h = $ height of mercury column
where ${P_A} = $ Pressure at the region above mercury inside the tube $= 0$
$ \Rightarrow {P_C} = {P_B} = 0 + \rho gh$
$\Rightarrow {P_a} = \rho gh$
At sea level ${P_a} = 1{\text{ }}atm$ and $h = 76{\text{ }}cm$
Therefore, $76{\text{ }}cm$ of mercury in a mercury barometer corresponds to the atmospheric pressure equivalent to one atmosphere. This value can be obtained by substituting the values of $\rho $, $g$ and $h$.
${P_a} = \left( {13.6 \times {{10}^{ - 3}}{\text{ }}kg{m^{ - 3}}} \right)\left( {9.8{\text{ }}m{s^{ - 2}}} \right)\left( {76{\text{ }}cm} \right)\\
\therefore {P_a}= 1.013 \times {10^5}{\text{ }}Pa$
Note: We can also find the standard atmospheric pressure from the help of an open tube manometer. In SI units the unit of pressure is $N{m^{ - 2}}$ or $Pascal\left( {Pa} \right)$. We can also find that the pressure increases as the height or the altitude gets on increasing and vice versa. Pressure is directly proportional to the force exerted and indirectly proportional to the surface area.
Complete answer:
Standard atmospheric pressure refers to the atmospheric pressure exerted by air on any unit surface area of substance. Let us find the atmospheric pressure using mercury barometer.
We can measure the atmospheric pressure at a point using a simple instrument called mercury barometer.
A long glass tube, closed at one end, is filled with mercury. It is then inverted over a trough containing mercury. Mercury in the tube slides down, till it becomes stable at a level. Due to this, the level of the mercury rises in the trough. When the level of the mercury becomes stable in the tube, we say that the pressure exerted by mercury is the same as the atmospheric pressure.
At sea level the mercury column in the barometer tube has a height of about above the mercury level in the trough.

Let us consider two points B and C at the same horizontal level as shown in the above figure. As they are at the same horizontal level, the same pressure acts at these points.
$ \Rightarrow {P_C} = {P_B} = {P_a}$ (atmospheric pressure)
But according to the expression for absolute pressure,
${P_B} = {P_A} + \rho gh$
Where, $\rho = $ density of mercury and $h = $ height of mercury column
where ${P_A} = $ Pressure at the region above mercury inside the tube $= 0$
$ \Rightarrow {P_C} = {P_B} = 0 + \rho gh$
$\Rightarrow {P_a} = \rho gh$
At sea level ${P_a} = 1{\text{ }}atm$ and $h = 76{\text{ }}cm$
Therefore, $76{\text{ }}cm$ of mercury in a mercury barometer corresponds to the atmospheric pressure equivalent to one atmosphere. This value can be obtained by substituting the values of $\rho $, $g$ and $h$.
${P_a} = \left( {13.6 \times {{10}^{ - 3}}{\text{ }}kg{m^{ - 3}}} \right)\left( {9.8{\text{ }}m{s^{ - 2}}} \right)\left( {76{\text{ }}cm} \right)\\
\therefore {P_a}= 1.013 \times {10^5}{\text{ }}Pa$
Note: We can also find the standard atmospheric pressure from the help of an open tube manometer. In SI units the unit of pressure is $N{m^{ - 2}}$ or $Pascal\left( {Pa} \right)$. We can also find that the pressure increases as the height or the altitude gets on increasing and vice versa. Pressure is directly proportional to the force exerted and indirectly proportional to the surface area.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Class 11 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

What is a periderm How does periderm formation take class 11 biology CBSE

What are porins class 11 biology CBSE

Why is steel more elastic than rubber class 11 physics CBSE

Differentiate between red algae and brown algae class 11 biology CBSE

What is boron A Nonmetal B Metal C Metalloid D All class 11 chemistry CBSE




