Question

Srivani walks $12m$ due East and turns Left and walks another $5m$, how far is she from the place she started?

Answer 1

Hint: Use Pythagoras theorem.

From figure,

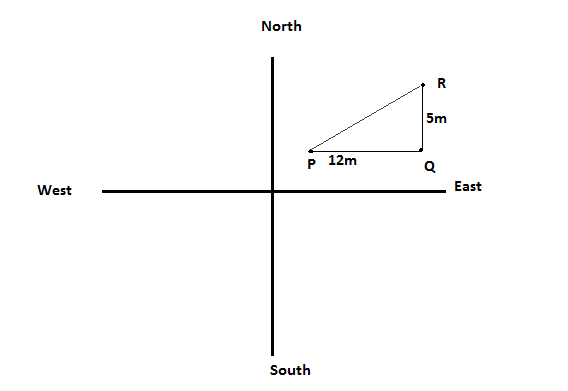
First sirvani starts from point P and moves $12m$ towards East then she reaches point Q. After she turns left it means her face was toward east direction on turning left side her face become towards North direction and walks $5m$ in North direction to reach point R.
Now, we have to find distance between P and R
You can easily see from the figure a right triangle formed.
So, we apply Pythagoras theorem
$
   \Rightarrow {\left( {PR} \right)^2} = {\left( {PQ} \right)^2} + {\left( {QR} \right)^2} \\
   \Rightarrow {\left( {PR} \right)^2} = {\left( {12} \right)^2} + {\left( 5 \right)^2} \\
   \Rightarrow {\left( {PR} \right)^2} = 144 + 25 = 169 \\
   \Rightarrow \left( {PR} \right) = \sqrt {169} = 13 \\
   \Rightarrow \left( {PR} \right) = 13m \\
 $

So, She is $13m$ far away from the starting point.

Note : In such types of problems always draw a figure with directions and move the point according to question. So, you can easily get an answer.