Question

$\square ABCD$ is a kite in which diagonal AC and diagonal BD intersect at point O. $\angle OBC = {20^0}$ and $\angle OCD = {40^0}$. Find $\angle ABC$

Answer 1

Hint: First we have to define what the terms we need to solve the problem are $\angle OBC$ is the right-angled triangle with the center B and with the angle of degree twenty.$\angle OCD$ is also the right-angled triangle with the center C and with the angle represented as forty; Since ABCD is the kite, which is flying on the air with the diagonal AC and diagonal BD will intersect at point O is the center overall.

Complete step-by-step solution:

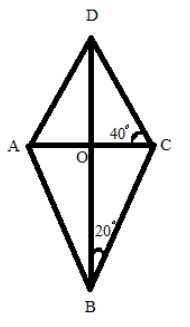
Since we can able to draw a diagram of the kite using the hints, as we see O is the center point for the kite and there is two right-angled triangle which is also given as $\angle OBC$ and $\angle OCD$ with the degree of ${20^0}$ and ${40^0}$ respectively. But also kite will have some other right angles like $\angle AOD$, $\angle DOC$, $\angle BOC$, $\angle AOB$and these right angles having ${90^0}$ at the center so all of these are the same \[\angle AOD = \angle DOC = \angle BOC = \angle AOB \Rightarrow {90^0}\]
Since we need to find $\angle ABC$, we will start with the right angle $\vartriangle OBC$ and this can be written as in the form of the right-angled triangle as $\angle BOC + \angle OBC + \angle OCB = {180^0}$(as we seen in the figure)
Substitute the know values we get ${90^0} + {20^0} + \angle OCB = {180^0}$ further solving we get $\angle OCB = {70^0}$
And since AB is equal to BC as they have the equal length in the adjacent hence $\angle ACB = \angle BAC = {70^0}$
Similarly for the second triangle $\vartriangle AOB$ is right angle triangle and we can rewrite this as $\angle ABO + \angle AOB + \angle OAB = {180^0}$ again substitute the known values $\angle ABO ={70^0} \text{ and } \angle AOB = {90^0}$ we get $\angle ABO = {20^0}$
Hence as we know $\angle ABC$ can be written as $\angle ABO + \angle OBC = {20^0} + {20^0} = {40^0}$ is the required degree for the given question.

Note: Since it was easy to calculate the degree of the triangle by applying the angle formulas, like $\vartriangle OBC$ (with center B) can be written as $\angle BOC + \angle OBC + \angle OCB = {180^0}$ (first with center O and with center B finally with center C). The total angle degree for every triangle(circle) is ${360^0}$. In this question, we only calculated the right angles which is half the total thus we used angles as ${180^0}$.