Question

What is the spring constant in parallel connection and series connection?

Answer 1

Hint: Two massless springs that follow Hooke's Law are said to be connected in parallel when they are connected by a thin, vertical rod, as shown in the diagram below. The formula for capacitors connected in parallel in an electrical circuit can be used to find the value of k.

Complete answer:
For parallel:

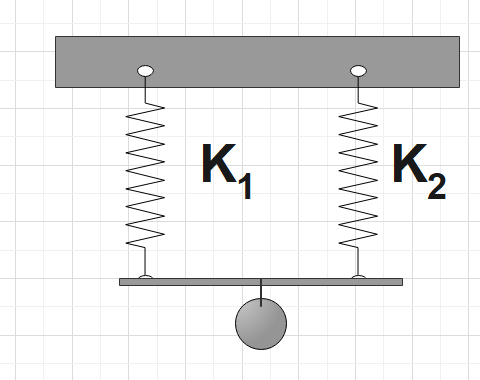
Two massless springs that follow Hooke's Law are said to be connected in parallel when they are connected by a thin, vertical rod.
 $k_{1}$ and $k_{2}$ are the spring constants for springs 1 and 2. The rod is subjected to a constant force $F$, which keeps it perpendicular to the force's direction. In order for the springs to be the same length. The springs could also be compressed if the force was reversed.
A single Hookean spring of spring constant $k$ is equivalent to this system of two parallel springs. The formula for parallel capacitors in an electrical circuit can be used to calculate the value of $k$.
$k=k_{1}+k_{2}$
For Series

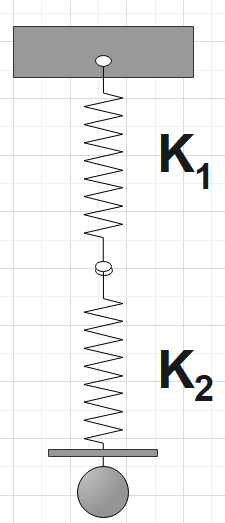
Here the equivalent spring constant would be,
$k=\dfrac{{{k}_{1}}{{k}_{2}}}{{{k}_{1}}+{{k}_{2}}}$
When the same springs are connected in series, as shown in the diagram below, this is referred to as a series connection. On spring 2, a constant force F is applied. As a result, the springs are elongated, and the total extension of the combination equals the sum of each spring's elongation. Alternatively, the springs could be compressed by reversing the force direction.
A single spring of spring constant k is equivalent to this system of two springs in series. The formula for capacitors connected in series in an electrical circuit can be used to calculate the value of k.

Note: When two or more springs are connected end-to-end or point-to-point in mechanics, they are said to be in series, and when they are connected side-by-side, they are said to be in parallel; in both cases, they act as a single spring.