Question

Split the following shapes into rectangles and find their areas. (The measures are given in centimeters.)

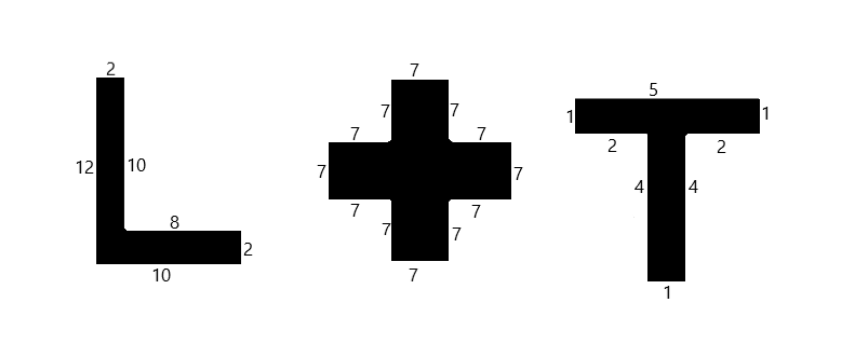
Answer 1

Hint: In this question, we are given three figures, one is of an L, the other is a plus sign and the third is a T. We are given the measurement of each side of the shapes. To find the area of such shapes we don’t have any formula, so we have to divide such figures into different basic figures whose areas can be calculated easily. Then we add all the areas to get the area of the whole shape.

Complete step-by-step answer:
It can be divided into rectangles as follows –

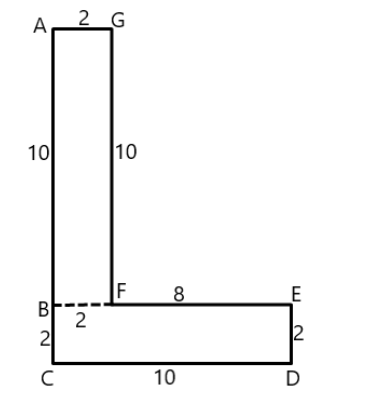
Area of rectangle ABFG $ =2\times 10=20c{{m}^{2}} $
Area of rectangle BCDE $ =2\times 10=20c{{m}^{2}} $
So, the area of the whole shape $ =20+20=40c{{m}^{2}} $
This shape can be divided into two rectangles as follows –

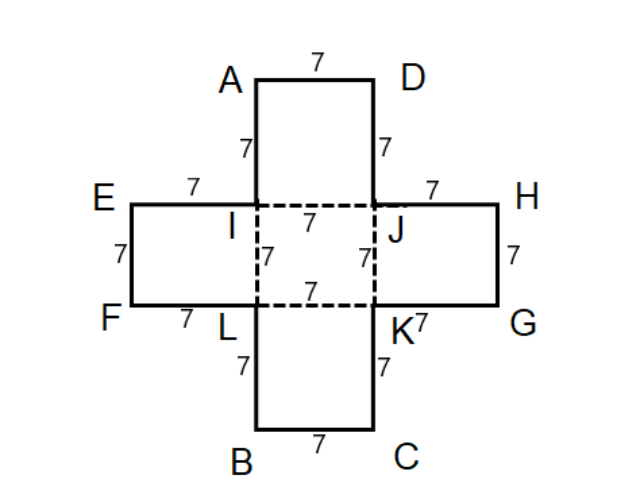
Area of rectangle ABCD $ =7\times \left( 7+7+7 \right)=147c{{m}^{2}} $
Area of the rectangle EFGH $ =7\times \left( 7+7+7 \right)=147c{{m}^{2}} $
But the whole will be determined by deleting the middle square part as it has been considered twice. The area of the middle square is $ =7\times 7=49c{{m}^{2}} $
So, Area of the whole shape $ =2\times 147-49=245c{{m}^{2}} $
This shape can be divided into two rectangles as follows –

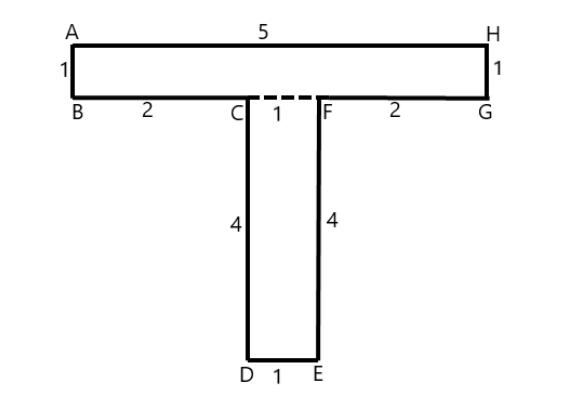
Area of the rectangle ABGH $ =5\times 1=5c{{m}^{2}} $
Area of the rectangle DEFC $ =4\times 1=4c{{m}^{2}} $
Area of the whole shape $ =5+4=9c{{m}^{2}} $

Note: We have divided the given shapes into rectangles by using the symmetry and properties of the rectangle. A rectangle is a 4-sided shape in which all the sides are perpendicular to each other and the opposite sides are always equal. A square is a special type of rectangle in which the adjacent sides are also equal. Using these properties we have divided the figure into several parts by the dotted lines.