Question

How do the special right triangles relate to the unit circle?

Answer 1

Hint: From the question given, we have been asked to relate the special right triangles to the unit circle. First of all, we have to know about the special right triangles and unit circle.
There are two types of special right triangles.
Type \[1\]: Triangle that is half of an equilateral triangle. Its three angle measures are \[{{30}^{\circ}},{{60}^{\circ}},{{90}^{\circ}}\]. And their side measures are \[a,\dfrac{a}{2},\dfrac{\sqrt{3}a}{2}\].
Type \[2\]: Triangle that has its side measures in the ratio of \[3:4:5\]. The proof is given by the Pythagoras theorem.
In mathematics, a unit circle is a circle of unit radius that is a circle of radius one.

Complete step by step answer:
Now considering from the question we have been asked to relate the special right triangles and unit circle.
From the basic concept we know that there are two types of special right angle triangles.
Type \[1\]: Triangle that is half of an equilateral triangle. Its three angle measures are \[{{30}^{\circ}},{{60}^{\circ}},{{90}^{\circ}}\]. And their side measures are \[a,\dfrac{a}{2},\dfrac{\sqrt{3}a}{2}\].
Type \[2\]: Triangle that has its side measures in the ratio of \[3:4:5\]. The proof is given by the Pythagoras theorem.
From the basic concept we know that the Pythagoras theorem states that the square of the longest side that is the hypotenuse is equal to the sum of the squares of the other two adjacent sides in a right angle triangle.
From the below represented figure, we can explain the relation between special right triangles and a unit circle.
Figure:

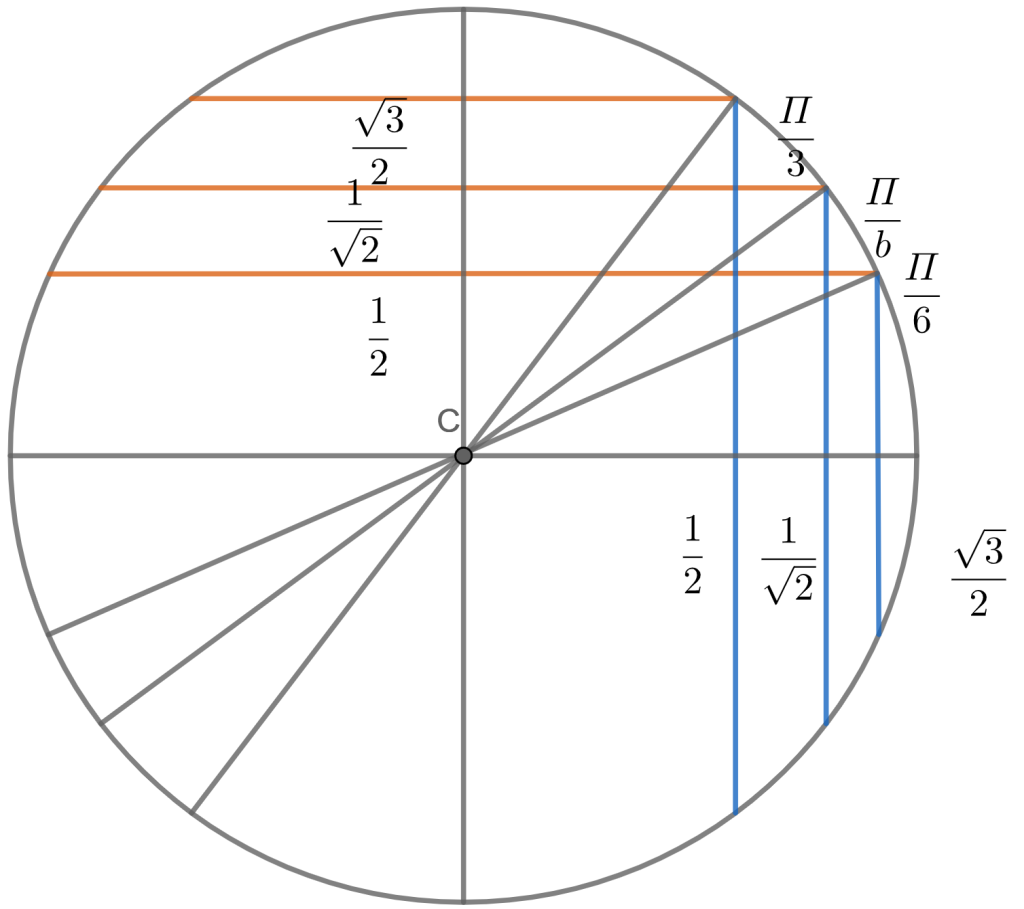
Each black and blue or black and red triangles is a special right angled triangle
The figures outside the circle: \[\dfrac{\pi }{6},\dfrac{\pi }{4},\dfrac{\pi }{3}\] are the angles that the triangles make with the horizontal axis.
\[\dfrac{1}{2},\dfrac{\sqrt{2}}{2},\dfrac{\sqrt{3}}{2}\] are the distances along the axes and the answers to \[\sin \left( x \right)\](yellow) and \[\cos \left( x \right)\](red) for each angle.
Hence, the special right triangles and the unit circle are related.

Note:
We should be well aware of the concept of special right triangles and unit circles. Also, we should be well known about the relation between special right triangles and unit circles. In this type of question, drawing a figure is the best solution for the question. We should draw the figure according to the question and then have to explain it. Similarly we can do this for any circle.