
When sound is produced in an aeroplane moving with a velocity of
A. 250 m
B.
C. 1250 m
D. 2500 m
Answer
504.9k+ views
Hint: To solve this problem, first divide the time taken to hear the echo by 2 as it is the time taken for the sound to go and come back. Then, use the formula for velocity giving relation between velocity and time. Using this formula, find the distance covered by aeroplane. Similarly, find the distance covered by sound. Using these values of distances, find the elevation of the aircraft.
Formula used:
Complete answer:
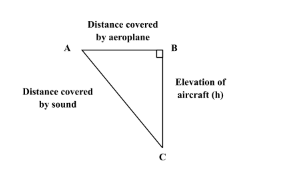
Let h be the elevation of the spacecraft.
Given: Velocity of aeroplane
Velocity of sound in air
Time for the echo (t) is given as
Velocity is given by,
Rearranging above equation we get,
Using equation. (1), distance covered by aeroplane is given by,
Substituting the values in above equation we get,
Similarly, distance covered by sound is given by,
Substituting the values in above equation we get,
From the figure, it can be inferred that,
Rearranging the above equation we get,
Substituting the values in above equation we get,
Taking the square root on both the sides we get,
Hence, the elevation of the aircraft is 2500 m.
So, the correct answer is “Option D”.
Note:
Students must remember to divide the time given by 2. As we have to consider time taken by sound to travel one-way. Students must also remember that the speed of sound for different mediums is different. So, if there was any other medium, the distance covered by sound would change depending on the density of the medium. Suppose the medium for sound to travel to be water. The sound travels faster in water, so the distance covered by the sound should be greater than what we got.
Formula used:
Complete answer:

Let h be the elevation of the spacecraft.
Given: Velocity of aeroplane
Velocity of sound in air
Time for the echo (t) is given as
Velocity is given by,
Rearranging above equation we get,
Using equation. (1), distance covered by aeroplane is given by,
Substituting the values in above equation we get,
Similarly, distance covered by sound is given by,
Substituting the values in above equation we get,
From the figure, it can be inferred that,
Rearranging the above equation we get,
Substituting the values in above equation we get,
Taking the square root on both the sides we get,
Hence, the elevation of the aircraft is 2500 m.
So, the correct answer is “Option D”.
Note:
Students must remember to divide the time given by 2. As we have to consider time taken by sound to travel one-way. Students must also remember that the speed of sound for different mediums is different. So, if there was any other medium, the distance covered by sound would change depending on the density of the medium. Suppose the medium for sound to travel to be water. The sound travels faster in water, so the distance covered by the sound should be greater than what we got.
Latest Vedantu courses for you
Grade 7 | CBSE | SCHOOL | English
Vedantu 7 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹45,300 per year
Recently Updated Pages
Master Class 11 Physics: Engaging Questions & Answers for Success

Master Class 11 Chemistry: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Class 11 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Trending doubts
Explain why it is said like that Mock drill is use class 11 social science CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

Net gain of ATP in glycolysis a 6 b 2 c 4 d 8 class 11 biology CBSE




