
Solving $ 1+{{\log }_{2}}\left( x-1 \right)\le {{\log }_{x-1}}4 $ we get domain of $ x $ be $ \left( m,n \right] $ .Find $ m+n $ . \[\]
Answer
563.4k+ views
Hint: We use the fact that the domain of logarithmic function is positive real number set to find $ m $ . We use logarithmic identities to make the function $ f\left( x \right)={{\log }_{2}}2\left( x-1 \right)-{{\log }_{x-1}}4 $ . We find for what $ x $ the function $ f\left( x \right)=0 $ and then use wavy curve method to find $ n $ . \[\]
Complete step by step answer:
We know that the logarithm is the inverse operation to exponentiation. If $ {{b}^{y}}=x $ then the logarithm denoted as log and calculated as with base $ b $ and argument $ x $ as
\[{{\log }_{b}}x=y\]
Here $ x,y,b $ are real numbers subjected to condition $ x>0 $ and $ b>0,b\ne 1 $ .We know the logarithmic identity involving power $ m\ne 0 $ where $ m $ is real number as
\[m{{\log }_{b}}x={{\log }_{b}}{{x}^{m}}\]
We also know the logarithmic identity involving product as
\[{{\log }_{b}}\left( mn \right)={{\log }_{b}}m+{{\log }_{b}}n\]
We are given
$ 1+{{\log }_{2}}\left( x-1 \right)\le {{\log }_{x-1}}4 $
We use the logarithmic identity $ {{\log }_{b}}b=1 $ for $ b=2 $ to have;
\[{{\log }_{2}}2+{{\log }_{2}}\left( x-1 \right)\le {{\log }_{x-1}}4\]
We use the logarithmic identity of product for $ m=2,n=x-1,b=2 $ in the left hand side of the above step to have;
\[\begin{align}
& {{\log }_{2}}2\left( x-1 \right)\le {{\log }_{x-1}}4 \\
& \Rightarrow {{\log }_{2}}2\left( x-1 \right)-{{\log }_{x-1}}4\le 0 \\
\end{align}\]
Let us define a function such that
\[f\left( x \right)={{\log }_{2}}2\left( x-1 \right)-{{\log }_{x-1}}4\]
We see that since logarithmic functions can take only positive real numbers as arguments we have $ 2\left( x-1 \right)>0\Rightarrow x>1 $ . Since the base cannot be negative or 1 we have again $ x-1>0\Rightarrow x>1 $ .So the minimum value for which $ f\left( x \right) $ is defined is 1 so we have $ m=1 $ . We need to find the zeroes of $ f\left( x \right) $ . So let us consider
\[f\left( x \right)={{\log }_{2}}2\left( x-1 \right)-{{\log }_{x-1}}4=0\]
We use trial and error methods to intuitively guess $ f\left( x \right)=0 $ when $ x-1=2 $ . So we have;
\[\begin{align}
& x-1=2 \\
& \Rightarrow x=3 \\
\end{align}\]
Since $ {{\log }_{2}}2\left( x-1 \right) $ and $ {{\log }_{x-1}}4 $ are strictly increasing curves they can intersect at most at one point and hence $ f\left( x \right) $ has only one zero and that is 3. So function $ f\left( x \right) $ will change the sign at $ x=3 $ . So let us draw the wavy curves
So the maximum value for which $ f\left( x \right)\le 0 $ is $ x=3 $ and hence $ n=3 $ . So we have
\[\begin{align}
& \left( m,n \right]=\left( 1,3 \right] \\
& \Rightarrow m+n=1+3=4 \\
\end{align}\]
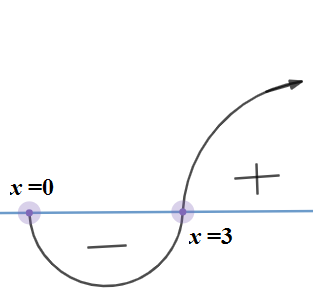
Note:
We can easily check that $ f\left( x \right)>0 $ for all $ x > 3 $ by putting $ x=5 $ in $ f\left( x \right) $ . We call a function strictly increasing when $ f\left( {{x}_{1}} \right) < f\left( {{x}_{2}} \right) $ implies $ {{x}_{1}} < {{x}_{2}} $ for all $ {{x}_{1}},{{x}_{2}} $ in the domain of $ f\left( x \right) $ . We call function monotonically increasing when $ f\left( {{x}_{1}} \right)\le f\left( {{x}_{2}} \right) $ implies $ {{x}_{1}}\le {{x}_{2}} $ .
Complete step by step answer:
We know that the logarithm is the inverse operation to exponentiation. If $ {{b}^{y}}=x $ then the logarithm denoted as log and calculated as with base $ b $ and argument $ x $ as
\[{{\log }_{b}}x=y\]
Here $ x,y,b $ are real numbers subjected to condition $ x>0 $ and $ b>0,b\ne 1 $ .We know the logarithmic identity involving power $ m\ne 0 $ where $ m $ is real number as
\[m{{\log }_{b}}x={{\log }_{b}}{{x}^{m}}\]
We also know the logarithmic identity involving product as
\[{{\log }_{b}}\left( mn \right)={{\log }_{b}}m+{{\log }_{b}}n\]
We are given
$ 1+{{\log }_{2}}\left( x-1 \right)\le {{\log }_{x-1}}4 $
We use the logarithmic identity $ {{\log }_{b}}b=1 $ for $ b=2 $ to have;
\[{{\log }_{2}}2+{{\log }_{2}}\left( x-1 \right)\le {{\log }_{x-1}}4\]
We use the logarithmic identity of product for $ m=2,n=x-1,b=2 $ in the left hand side of the above step to have;
\[\begin{align}
& {{\log }_{2}}2\left( x-1 \right)\le {{\log }_{x-1}}4 \\
& \Rightarrow {{\log }_{2}}2\left( x-1 \right)-{{\log }_{x-1}}4\le 0 \\
\end{align}\]
Let us define a function such that
\[f\left( x \right)={{\log }_{2}}2\left( x-1 \right)-{{\log }_{x-1}}4\]
We see that since logarithmic functions can take only positive real numbers as arguments we have $ 2\left( x-1 \right)>0\Rightarrow x>1 $ . Since the base cannot be negative or 1 we have again $ x-1>0\Rightarrow x>1 $ .So the minimum value for which $ f\left( x \right) $ is defined is 1 so we have $ m=1 $ . We need to find the zeroes of $ f\left( x \right) $ . So let us consider
\[f\left( x \right)={{\log }_{2}}2\left( x-1 \right)-{{\log }_{x-1}}4=0\]
We use trial and error methods to intuitively guess $ f\left( x \right)=0 $ when $ x-1=2 $ . So we have;
\[\begin{align}
& x-1=2 \\
& \Rightarrow x=3 \\
\end{align}\]
Since $ {{\log }_{2}}2\left( x-1 \right) $ and $ {{\log }_{x-1}}4 $ are strictly increasing curves they can intersect at most at one point and hence $ f\left( x \right) $ has only one zero and that is 3. So function $ f\left( x \right) $ will change the sign at $ x=3 $ . So let us draw the wavy curves
So the maximum value for which $ f\left( x \right)\le 0 $ is $ x=3 $ and hence $ n=3 $ . So we have
\[\begin{align}
& \left( m,n \right]=\left( 1,3 \right] \\
& \Rightarrow m+n=1+3=4 \\
\end{align}\]
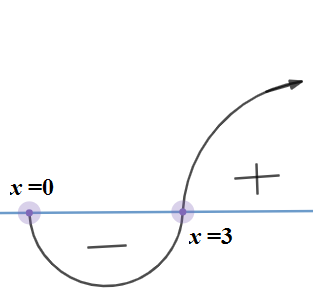
Note:
We can easily check that $ f\left( x \right)>0 $ for all $ x > 3 $ by putting $ x=5 $ in $ f\left( x \right) $ . We call a function strictly increasing when $ f\left( {{x}_{1}} \right) < f\left( {{x}_{2}} \right) $ implies $ {{x}_{1}} < {{x}_{2}} $ for all $ {{x}_{1}},{{x}_{2}} $ in the domain of $ f\left( x \right) $ . We call function monotonically increasing when $ f\left( {{x}_{1}} \right)\le f\left( {{x}_{2}} \right) $ implies $ {{x}_{1}}\le {{x}_{2}} $ .
Recently Updated Pages
Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Class 11 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The draft of the Preamble of the Indian Constitution class 10 social science CBSE

Who gave "Inqilab Zindabad" slogan?

Write a letter to the principal requesting him to grant class 10 english CBSE

Who was Subhash Chandra Bose Why was he called Net class 10 english CBSE




