
Solve \[x - 3\left( {2 + x} \right) > 2\left( {3x - 1} \right),x \in \left| { - 3, - 2, - 1,0,1,2} \right|\] . Also represent its solution on the number line.
Answer
563.1k+ views
Hint: Here, we will solve for the given variable. We will solve the inequality by using the arithmetic operations and we will get the required answer. The solution for this inequality has to be represented on a number line. An inequality is defined as a non-equal comparison between two numbers or expressions with the variables which may be greater than or lesser than or greater than equal to or less than equal to.
Complete step-by-step answer:
We are given an inequality \[x - 3\left( {2 + x} \right) > 2\left( {3x - 1} \right)\].
By multiplying the terms, we get
\[ \Rightarrow x - 6 - 3x > 6x - 2\]
Taking the like terms on one side of the equation, we get
\[ \Rightarrow x - 6x - 3x > 6 - 2\]
By adding the like terms, we get
\[ \Rightarrow x - 9x > 6 - 2\]
By subtracting the like terms, we get
\[ \Rightarrow - 8x > 4\]
By rewriting the equation, we get
\[ \Rightarrow x > \dfrac{4}{{ - 8}}\]
By dividing the numbers, we get
\[ \Rightarrow x > \dfrac{{ - 1}}{2}\]
\[ \Rightarrow x > - 0.5\]
We are given that \[x \in \left| { - 3, - 2, - 1,0,1,2} \right|\]
So, we get
\[ \Rightarrow x = - 1, - 2, - 3\] since \[x > - 0.5\]
Now we will represent the solution on the number line.
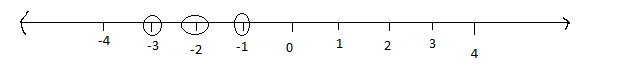
Therefore, the values of \[x\] are \[ - 3, - 2, - 1\].
Note: Here, we have added the like terms of the given inequality. We should remember that adding the same quantity on both the sides of an inequality does not change its direction. When we multiply or divide the positive number there is no change in the direction. When we multiply or divide by a negative number, there is a change in the direction of an inequality. We have also used the distributive property of multiplication to simplify the terms. Distribution property states that if a number is multiplied to the sum of two numbers then it is given by \[a \cdot \left( {b + c} \right) = ab + ac\].
Complete step-by-step answer:
We are given an inequality \[x - 3\left( {2 + x} \right) > 2\left( {3x - 1} \right)\].
By multiplying the terms, we get
\[ \Rightarrow x - 6 - 3x > 6x - 2\]
Taking the like terms on one side of the equation, we get
\[ \Rightarrow x - 6x - 3x > 6 - 2\]
By adding the like terms, we get
\[ \Rightarrow x - 9x > 6 - 2\]
By subtracting the like terms, we get
\[ \Rightarrow - 8x > 4\]
By rewriting the equation, we get
\[ \Rightarrow x > \dfrac{4}{{ - 8}}\]
By dividing the numbers, we get
\[ \Rightarrow x > \dfrac{{ - 1}}{2}\]
\[ \Rightarrow x > - 0.5\]
We are given that \[x \in \left| { - 3, - 2, - 1,0,1,2} \right|\]
So, we get
\[ \Rightarrow x = - 1, - 2, - 3\] since \[x > - 0.5\]
Now we will represent the solution on the number line.
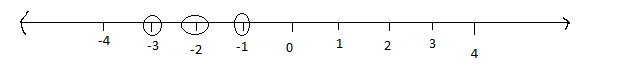
Therefore, the values of \[x\] are \[ - 3, - 2, - 1\].
Note: Here, we have added the like terms of the given inequality. We should remember that adding the same quantity on both the sides of an inequality does not change its direction. When we multiply or divide the positive number there is no change in the direction. When we multiply or divide by a negative number, there is a change in the direction of an inequality. We have also used the distributive property of multiplication to simplify the terms. Distribution property states that if a number is multiplied to the sum of two numbers then it is given by \[a \cdot \left( {b + c} \right) = ab + ac\].
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Complete reduction of benzene diazonium chloride with class 12 chemistry CBSE

How can you identify optical isomers class 12 chemistry CBSE

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Convert 40circ C to Fahrenheit A 104circ F B 107circ class 8 maths CBSE

Advantages and disadvantages of science

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE





