Question

How to solve two absolute value inequalities $\left| x+1 \right|+\left| x-1 \right|\le 2$ ?

Answer 1

Hint: To solve the above inequality we are going to first find the critical points means where the modulus becomes 0. So, equate the functions in x written in modulus to 0. Then we are going to draw the graph of $\left| x+1 \right|+\left| x-1 \right|$ using the critical functions and then see the interval of x where the value of this modulus function $\left| x+1 \right|+\left| x-1 \right|$ takes value 2 or less than that.

Complete step by step solution:
 The inequality given in the above problem is as follows:
$\left| x+1 \right|+\left| x-1 \right|\le 2$
First of all, we are going to draw the graph of $\left| x+1 \right|+\left| x-1 \right|$. For that, we are going to find the critical points of this function and that we do by equating each expressions in x written in the modulus to 0 so equating $\left( x+1 \right)\And \left( x-1 \right)$ to 0 we get,
$\begin{align}
  & x+1=0 \\
 & \Rightarrow x=-1; \\
 & x-1=0 \\
 & \Rightarrow x=1 \\
\end{align}$
Hence, we got two critical points in x which are (1 & -1).
Now, we are going to find the values of the modulus function written on the L.H.S of the given inequality at critical points. At $x=-1$, we are going to find the value the function as follows:
$\begin{align}
  & \Rightarrow \left| -1+1 \right|+\left| -1-1 \right| \\
 & =0+\left| -2 \right| \\
\end{align}$
And we know that when we apply modulus on any function then only positive value of that number comes out so we get the evaluation of the above modulus as:
$=2$
Now, substituting $x=1$ in the above modulus function we get,
$\begin{align}
  & \Rightarrow \left| 1+1 \right|+\left| 1-1 \right| \\
 & =\left| 2 \right|+0 \\
 & =2 \\
\end{align}$
Now, when x is less than -1 then the whole function gives a positive value. Similarly when x is greater than 1 then the whole function is positive and when x lies in between and equal to -1 to 1 the function will take a constant value i.e. 2. So, the graph of the function looks as follows:

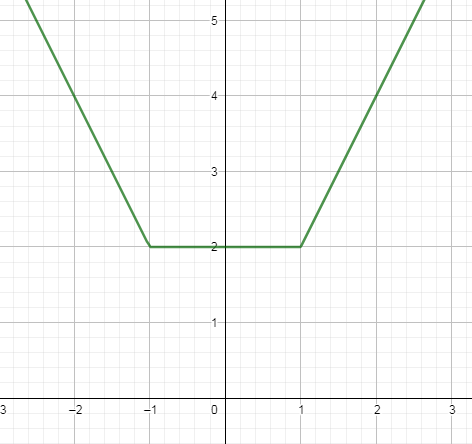
Now, we have to find the solution set when the above graph will take value 2 or less than that which can be possible when we take the interval of x from -1 to 1. So, the answer to the above problem is as follows:
$-1\le x\le 1$

Note: In the above problem, if we have asked to find the solution set for the following inequality:
$\left| x+1 \right|+\left| x-1 \right|\ge 2$
Now, we have only changed the sign of the inequality and all the expressions are constant.
To solve this kind of inequality, we are going to see the graph of $\left| x+1 \right|+\left| x-1 \right|$ which we are again showing:

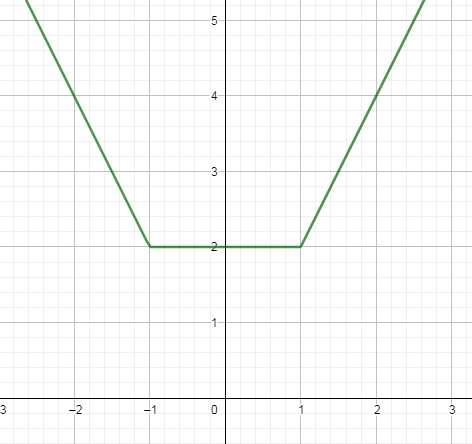
Now, from the graph you can see that the above function is taking value 2 or greater than that when x is less than or equal to -1 and when x is greater than and equal to 1. Hence, the solution set for the above problem is as follows:
$x\in (-\infty ,-1]\bigcup [1,\infty )$
The open bracket is showing infinity is not included and the closed bracket is showing that number has been included.