Question

How do you solve this problem $4.\ln x=\ln 2x$ ?

Answer 1

Hint: This type of question can be solved by using the basic rules for the logarithmic function. We apply those rules and simplify the equation to its simplest form and then obtain the solution.

Complete step-by-step answer:
The question is given as $4.\ln x=\ln 2x$ . We need to first simplify this equation.
We all know the log of power rule which is stated as,
$\Rightarrow y\ln (x)=\ln ({{x}^{y}})$
Using this to the LHS,
$\begin{align}
  & \Rightarrow 4.\ln x=\ln 2x \\
 & \Rightarrow \ln ({{x}^{4}})=\ln 2x \\
\end{align}$
We then take both the terms to one side as,
$\Rightarrow \ln ({{x}^{4}})-\ln 2x=0......(1)$
The quotient rule for ln functions is given as,
$\Rightarrow \ln \left( \dfrac{x}{y} \right)=\ln (x)-\ln (y)......(2)$
Using the same rule in the above equation (1), we get
$\Rightarrow \ln \left( \dfrac{{{x}^{4}}}{2x} \right)=0......(3)$
We know that ln is nothing but the log function with a base e instead of a base 10, that is
$\Rightarrow \ln x={{\log }_{e}}x$
And we also know that log can be represented as follows too,
$\begin{align}
  & \Rightarrow {{\log }_{a}}x=n......(4) \\
 & \Rightarrow {{a}^{n}}=x......(5) \\
\end{align}$
From all the above information, we first convert equation (3) into log format.
$\Rightarrow {{\log }_{e}}\left( \dfrac{{{x}^{4}}}{2x} \right)=0$
Using equations (4) and (5) we convert it to the form as given in equation (5).
$\Rightarrow \left( \dfrac{{{x}^{4}}}{2x} \right)={{e}^{0}}$
We know that ${{e}^{0}}=1$ and the we cross multiply the denominator on the LHS with the RHS.
$\Rightarrow \left( \dfrac{{{x}^{4}}}{2x} \right)=1$
Cancelling an x term from numerator and denominator,
$\Rightarrow {{x}^{3}}=2......(6)$
Simplifying this equation (6) further by cancelling x on both sides,
$\begin{align}
  & \Rightarrow x=\sqrt[3]{2} \\
 & \Rightarrow x=1.259921 \\
\end{align}$
Rounding it off to 4 digits,
$\Rightarrow x=1.2599$
Hence the solution to the above equation is $x=1.2599$ .
We can plot the graph for the equation (6).

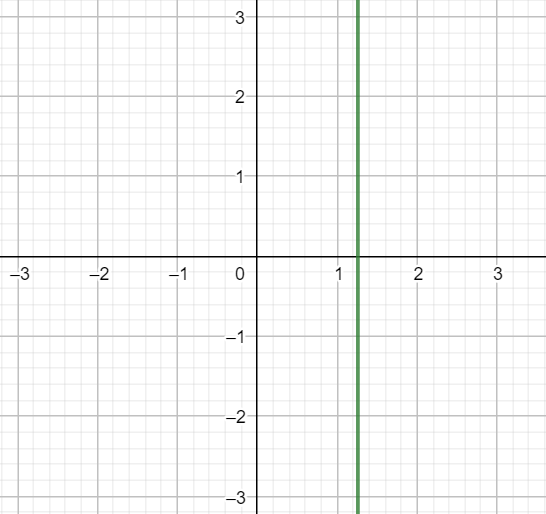
Here we see the solution at the point $x=1.2599$ .
Hence the solution to the given problem is $x=1.2599$ .

Note: While solving this question, the students need to be careful while applying the logarithmic rules. There is another method to solve this- They can cancel both the ln functions on both sides of the equation and they remain with x and 2x separated by an equal sign. It gives the same result as above. They can verify the same by plotting the graph for the same.