Question

How to solve this inequation ?
${{x}^{4}}-{{x}^{3}}-x>0$

Answer 1

Hint: To solve this question, we need to know the concept of inequalities. Given in the question is the inequality ${{x}^{4}}-{{x}^{3}}-x>0.$ We solve this question just like how we solve for a normal polynomial equation. We equate this equation to 0 and find its roots by factorization. These roots are also called the critical points of the equation. After finding the points, since the function is greater than 0, we consider all the roots outside the range of these two roots.

Complete step by step solution:
In order to solve such questions, it is very important to know concepts of inequalities and how to solve them to obtain a solution. The inequality given in the question is
$\Rightarrow {{x}^{4}}-{{x}^{3}}-x>0$
We are now required to find the critical points of this inequality. We do this by equating the function of the inequality to zero and solving by factorization.
$\Rightarrow {{x}^{4}}-{{x}^{3}}-x=0$
Taking x common out and factoring,
$\Rightarrow x\left( {{x}^{3}}-{{x}^{2}}-1 \right)=0$
Equate each of these factors to 0 individually,
$\Rightarrow x=0$
$\Rightarrow {{x}^{3}}-{{x}^{2}}-1=0$
One of the solutions is 0. For the other solution, we need to solve the second equation. This equation cannot be factored further, and we find out the solution to this equation ${{x}^{3}}-{{x}^{2}}-1=0$ is x=1.4655.
Therefore, we know that since the given inequation has its function value greater than 0, the solution to this equation can be given outside the range of $\left( 0,1.4655 \right)$ that is, $x<0$ and $x>1.4655.$
These regions can be plotted in a graph as shown in the figure below. The shaded region right of the point at which $x=1.4655$ and the shaded region to the left of the point $x=0$ represent the solution to the given question.

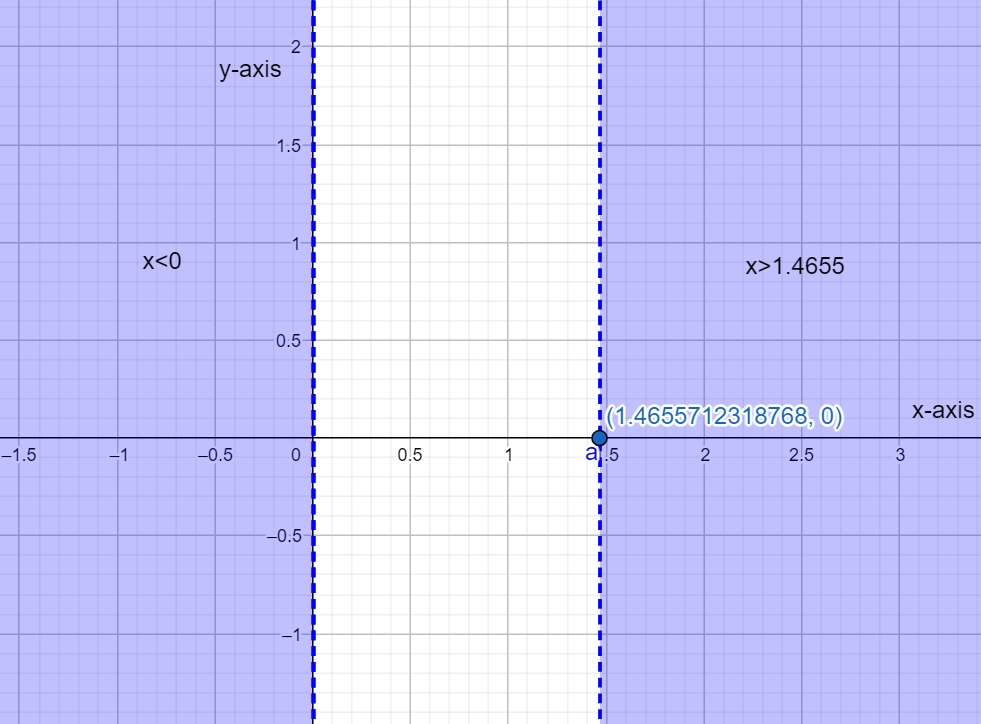
Hence, the solution to the inequation ${{x}^{4}}-{{x}^{3}}-x>0$ is given by $x<0$ and $x>1.4655.$

Note: It is important to know the concepts of factorization in order to solve a polynomial equation. Without this, finding the roots becomes difficult. In case the polynomial cannot be factored further, we can approximately plot the curve and figure out the root for the equation.