Question

How do you solve the two step inequality $7x-4>3x+8?$

Answer 1

Hint: We will transpose the terms accordingly so that the similar terms lie on the same side of the inequality. Only the similar terms can be added or subtracted. We will further transpose the terms if it is required.

Complete step by step answer:
Consider the inequality given $7x-4>3x+8.$
Now, in the above inequality, we can see that both the left-hand side and the right-hand side contain the terms including the variable $x$ with exponent $1.$ On the left-hand side the term containing $x$ is $7x$ and on the right-hand side the term the term containing $x$ is $3x.$
Also, it is seen that both the left-hand side and the right-hand side contain constant terms. On the right-hand side, the constant term is $8$ and on the left-hand side, the constant term is $-4.$
So, we transpose the constant term $-4$ from the left-hand side to the right-hand side of the inequality while we transpose the variable term $3x$ from the right-hand side to the left-hand side of the inequality.
Now, on the left-hand side the term $3x$ will become $-3x.$ On the right-hand side the term $-4$ will become $+4.$
Let us do the process step by step so that we do not have any confusion.
Let us transpose $3x$ to get $7x-3x-4>8.$
Now, we transpose $-4$ to get $7x-3x>8+4.$
We know that we can add or subtract the coefficients of the variable terms while the variable remains the same.
So, we will get $4x>12.$
Now we will transpose $4$ to get $x>\dfrac{12}{4}=3.$

Hence the solution is $x>3.$

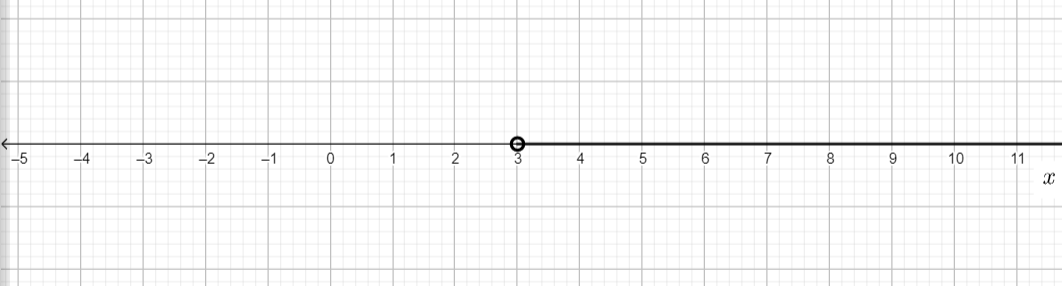
Note: From the solution obtained, we can learn that the given inequality is true for all the values of $x$ that are greater than $3.$ We should not forget to change the signs when we transpose the terms from one side to the other. Negative will become positive and positive will become negative. Also, remember that the inequality changes when the whole inequality is multiplied by $-1.$ That is, when we multiply the whole inequality with $-1,$ $<$ changes to $>$ and $>$ changes to $<.$ Given below is the graph that represents the values of $x$ that satisfies the inequality, that is, $x>3:$