Question

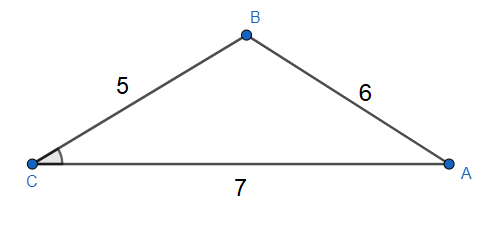
How do you solve the triangles when the sides of $a=5,b=7,c=6$. Find the other sides and measurement of angles.

Answer 1

Hint: We first need to find the value of $2R$ where $2R=\dfrac{abc}{2\Delta }$. We also use the relation $\Delta =\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$. After getting the values we use \[\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=2R\] to find the angles.

Complete step by step solution:
We have been given the values of three sides’ length.
We are going to use the relation for properties of triangles between angles and sides of a general triangle.
If we take $R$ as the circum-radius of the triangle then we have $2R=\dfrac{abc}{2\Delta }$ where $\Delta =\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$, the area of the triangle.
Here $s$ represents the semi-perimeter of the triangle. So, $2s=a+b+c$.
Putting the values $a=5,b=7,c=6$, we get \[s=\dfrac{a+b+c}{2}=\dfrac{5+7+6}{2}=\dfrac{18}{2}=9\].

We put the value of $s$ in $\Delta =\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$ and get
$\Delta =\sqrt{9\left( 9-5 \right)\left( 9-7 \right)\left( 9-6 \right)}=\sqrt{216}=6\sqrt{6}$.
Now we put the value of $\Delta $ in $2R=\dfrac{abc}{2\Delta }$.
So, $2R=\dfrac{abc}{2\Delta }=\dfrac{5\times 6\times 7}{2\times 6\sqrt{6}}=\dfrac{35}{2\sqrt{6}}$.
The theorem of properties of triangle gives that for $\Delta ABC$, we have \[\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=2R\] where $a,b,c$ are the lengths of the sides and $A,B,C$ are corresponding opposite angles of the sides $a,b,c$ respectively.
We have been given that $a=5,b=7,c=6$ and $2R=\dfrac{35}{2\sqrt{6}}$.
We put these values in the equation to get \[\dfrac{5}{\sin A}=\dfrac{7}{\sin B}=\dfrac{6}{\sin C}=\dfrac{35}{2\sqrt{6}}\].
We get first linear equation of \[\dfrac{5}{\sin A}=\dfrac{35}{2\sqrt{6}}\].
Solving the equation, we get \[\sin A=\dfrac{5\times 2\sqrt{6}}{35}=\dfrac{2\sqrt{6}}{7}\].
Taking trigonometric inverse, we get $\angle A={{44.41}^{\circ }}$.
We get a second linear equation of \[\dfrac{6}{\sin C}=\dfrac{35}{2\sqrt{6}}\].
Solving the equation, we get \[\sin C=\dfrac{6\times 2\sqrt{6}}{35}=\dfrac{12\sqrt{6}}{35}\].
Taking trigonometric inverse, we get $\angle C={{57.12}^{\circ }}$.
We get the first linear equation of \[\dfrac{7}{\sin B}=\dfrac{35}{2\sqrt{6}}\].
Solving the equation, we get \[\sin B=\dfrac{7\times 2\sqrt{6}}{35}=\dfrac{2\sqrt{6}}{5}\].
Taking trigonometric inverse, we get $\angle B={{78.47}^{\circ }}$.
Therefore, the angles are $\angle A={{44.41}^{\circ }},\angle B={{78.47}^{\circ }},\angle C={{57.12}^{\circ }}$.

Note: To find the third angle for the triangle we also could have used the relation of the angles of a triangle where we get the sum of all the angles as ${{180}^{\circ }}$.
So, $\angle A+\angle B+\angle C={{180}^{\circ }}$ which gives $\angle B={{180}^{\circ }}-\angle A-\angle C$.
We put the values to get \[\angle B={{180}^{\circ }}-{{44.41}^{\circ }}-{{57.12}^{\circ }}={{78.47}^{\circ }}\].