Question

How do you solve the system ${x^2} + {y^2} = 7$ and $y = x - 7$?

Answer 1

Hint: First we have to replace all occurrences of $y$ in ${x^2} + {y^2} = 7$ with $x - 7$. Next, we have to expand the parenthesis using algebraic identity. Next, we have to divide both sides of the equation by $2$. Next, we have to compare the obtained quadratic equation to the standard quadratic equation and find the value of numbers $a$, $b$ and $c$. Finally, substitute the values of $a$, $b$ and $c$ in $D = {b^2} - 4ac$ and find the discriminant of the given equation, then we will get the desired result.

Formula used:
Algebraic Identity:
${\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}$……(i)
Where, $a$and $b$are any two numbers.
The quantity $D = {b^2} - 4ac$ is known as the discriminant of the equation $a{x^2} + bx + c = 0$ and its roots are given by
$x = \dfrac{{ - b \pm \sqrt D }}{{2a}}$or $x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}$……(ii)
The numbers $a$, $b$ and $c$ are called the coefficients of the equation.

Complete step by step solution:
First, we have to replace all occurrences of $y$ in ${x^2} + {y^2} = 7$ with $x - 7$.
${x^2} + {\left( {x - 7} \right)^2} = 7$
Now, we have to expand above parenthesis using algebraic identity (i).
$ \Rightarrow {x^2} + {x^2} - 14x + 49 = 7$
$ \Rightarrow 2{x^2} - 14x + 42 = 0$
Now, we have to divide both sides of the equation by $2$.
${x^2} - 7x + 21 = 0$
Now we have to compare the above quadratic equation to the standard quadratic equation and find the value of numbers $a$, $b$ and $c$.
Comparing ${x^2} - 7x + 21 = 0$ with $a{x^2} + bx + c = 0$, we get
$a = 1$, $b = - 7$ and $c = 21$
Now, we have to substitute the values of $a$, $b$ and $c$ in $D = {b^2} - 4ac$ and find the discriminant of the given equation.
$D = {\left( { - 7} \right)^2} - 4\left( 1 \right)\left( {21} \right)$
After simplifying the result, we get
$ \Rightarrow D = 49 - 84$
$ \Rightarrow D = - 35$
Which means the given equation has no real roots.

Final solution: Hence, the given system of equations has no solutions.

Note:
In the above question, we can find the solution by drawing the circle and equation of line on graph paper and check whether they intersect or not.

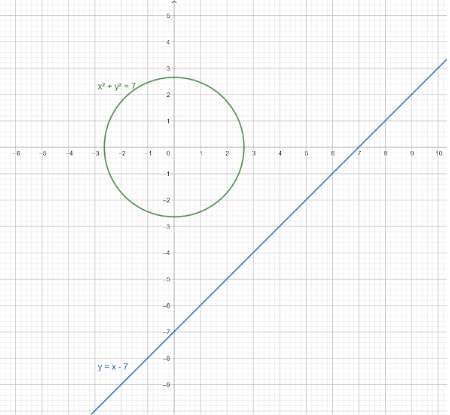
Since, the two graphs never intersect, this confirms our conclusion of no solution.