Question

How do you solve the system of linear equations $3x+2y=6$ and $x+2y=-6$ .

Answer 1

Hint: Now to find the solution of the given equation we will first plot the lines represented by the given equations. To find the lines we will substitute the values of x and find corresponding values of y for the equations. Now we will plot the points (x, y) such and draw a line passing through them. Now after plotting both lines in this manner we will find the intersection point of the two lines. This intersection point is the solution of the given equations.

Complete step by step solution:
Now consider the given system of linear equations $3x+2y=6$ and $x+2y=-6$ .
First let us understand what it means to find the solution of a system of linear equations.
Now the solution of the system of linear equations means to find the values of x and y such that the values satisfy both the equations simultaneously.
Hence if the equation represents straight lines in XY planes the solution is nothing but the intersection point of the two lines.
Now we will solve the equation by geometric method.
The given equation $3x+2y=6$
Now on substituting x = 0 in the equation we get $2y=6$
Hence we can say that if x = 0 then y = 3.
Ow similarly on substituting y = 0 we get $3x=6$
Hence when we have y = 0 we get x = 2.
Hence the points (0, 3) and (2, 0) lie on the line.
Now we will plot the two points and draw a line passing through all the points.
Hence we get,

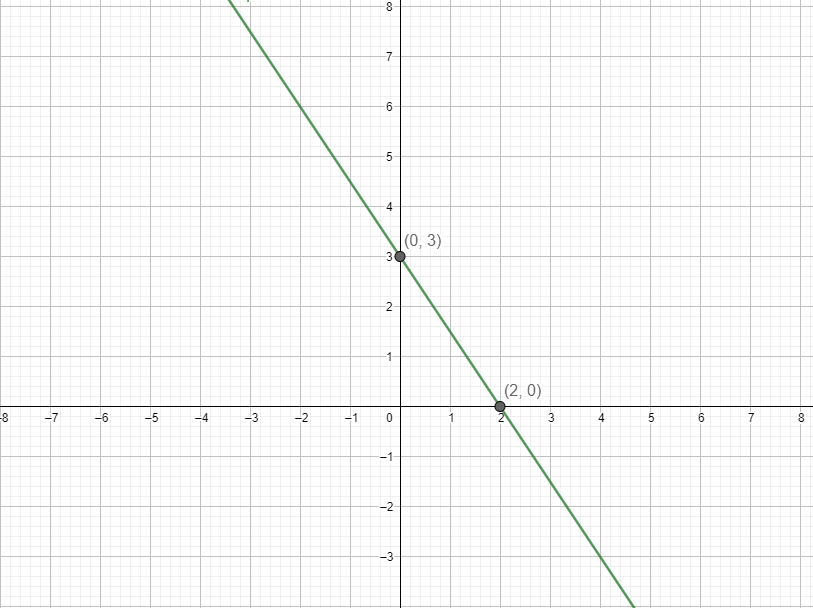
Now similarly consider the equation $x+2y=-6$ .
Now on substituting x = 0 in the equation we get $2y=-6$
Hence on x = 0 we have y = - 3.

Now on substituting y = 0 we get x = - 6.
Hence the point (0, -3) and (-6, 0) lies on the line represented by the equation $x+2y=-6$
Now let us plot the points on the graph and pass the line passing through the points.
Hence, we get

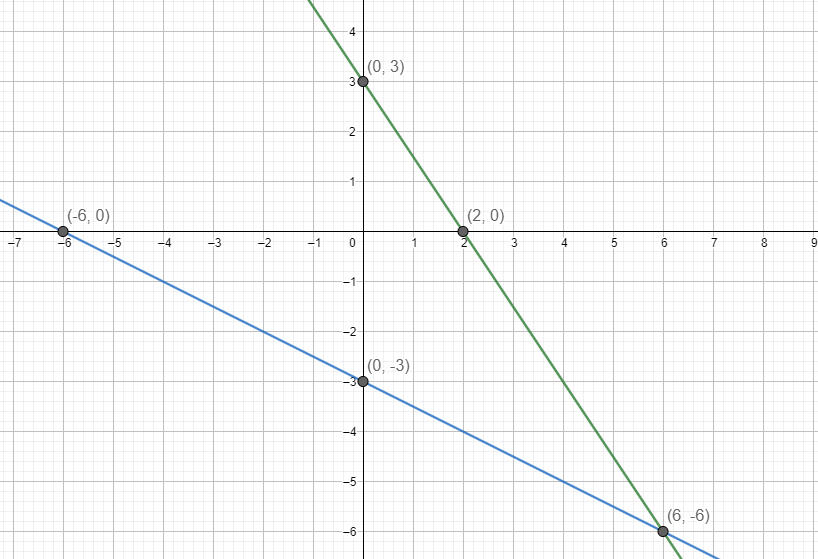
Now we can see that the two lines intersect at points (6, -6).

Hence the solution of the equation is x = 6 and y = - 6.

Note: Now note that we can also solve the equation algebraically. To solve the equation algebraically we will multiply the equations with appropriate scalars such that the coefficient of one variable in both equations is equal. Then we will add or subtract the equations to eliminate a variable and hence get a linear equation. Now solving this we will get the value of one variable. Substituting the value in any equation we get the value of another variable.